标签：产生   样本   注意   函数   采样   模型   公式   技术   new   

概述

通俗来讲，最大似然估计，就是利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

重要的假设是所有采样满足独立同分布。

求解模型参数过程

假如我们有一组连续变量的采样值（x1,x2,…,xn），我们知道这组数据服从正态分布，标准差已知。请问这个正态分布的期望值为多少时，产生这个已有数据的概率最大？

　　　　P(Data | M) = ？

根据公式

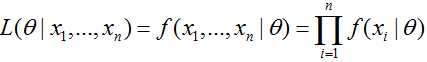
　　可得: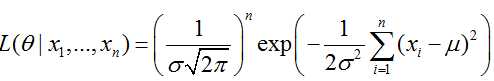

　　对μ求导可得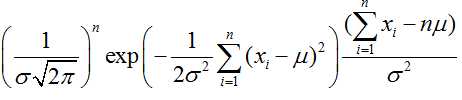 ,则最大似然估计的结果为μ=(x1+x2+…+xn)/n

由上可知最大似然估计的一般求解过程：

　　（1） 写出似然函数；

　　（2） 对似然函数取对数，并整理；

　　（3） 求导数 ；

　　（4） 解似然方程

注意：最大似然估计只考虑某个模型能产生某个给定观察序列的概率。而未考虑该模型本身的概率。这点与贝叶斯估计区别。贝叶斯估计方法将在以后的博文中描述

『科学计算_理论』最大似然估计

标签：产生   样本   注意   函数   采样   模型   公式   技术   new   

原文地址：http://www.cnblogs.com/hellcat/p/7206546.html