标签:3.3 最小 定义函数 中序 inline 3.1 == har 一个栈
我们计算一个数的时候, 用到的式子就是表达式, 例如 $2 + 3 \times 4$ 就是一个表达式.
表达式有三种: 前缀表达式, 中缀表达式, 后缀表达式.
前缀表达式, 就是形如 " 运算符 数字 数字 " 的表达式. 例如 $+~2~2~=~4$ .
中缀表达式, 就是形如 " 数字 运算符 数字 " 的表达式. 例如 $2~+~2~=~4$ .
后缀表达式, 就是形如 " 数字 数字 运算符 " 的表达式. 例如 $2~2~+~=~4$ .
中缀表达式是我们日常生活中用的, 最直观, 运算有优先级.
前缀表达式和后缀表达式的出现在于它们的优点: 没有优先级, 编程难度低!
既然给出了前缀表达式, 中缀表达式, 后缀表达式的概念.
我们就尝试提出一些问题, 并对这些问题进行解决.
(1) 给定前缀表达式, 中缀表达式, 后缀表达式, 如何用编程实现求值?
(2) 如何实现前缀表达式, 中缀表达式, 后缀表达式间的相互转化?
前缀表达式恰好是后缀表达式的逆序, 可以互相转化.
也就是说, 前缀表达式已经无关紧要了, 关键实现后缀表达式与中缀表达式的转化.
假如从左往右扫描中缀表达式, 由于运算符优先级的问题, 可能会先运算后面, 再运算前面.
于是我们考虑维护两个栈, 一个栈存运算符, 一个栈存数字.
当遇到一个数字的时候, 把数字压入栈中.
当遇到一个运算符的时候, 将前面的优先级高的运算符和数字先提出来运算, 然后再插入这个运算符.
// ^: 0 *: 1 +, -: 2 ): 3 (: 4 const char bond[5][5] = { ‘>‘, ‘>‘, ‘>‘, ‘>‘, ‘.‘, ‘.‘, ‘>‘, ‘>‘, ‘>‘, ‘.‘, ‘.‘, ‘.‘, ‘>‘, ‘>‘, ‘.‘, ‘.‘, ‘.‘, ‘.‘, ‘.‘, ‘.‘, // 根本不会出现在栈中 ‘.‘, ‘.‘, ‘.‘, ‘.‘, ‘.‘, }; // > :先计算前面的 // . : 先不动 int id[500]; inline char rdc(void) { char c = getchar(); for (; c == ‘ ‘; c = getchar()); return c; } inline int compute(int x, int y, char c) { if (c == ‘+‘) return (x + y) % MOD; else if (c == ‘-‘) return ((x - y) % MOD + MOD) % MOD; else if (c == ‘*‘) return 1LL * x * y % MOD; else if (c == ‘^‘) { int ans = 1; for (; y > 0; y >>= 1, x = 1LL * x * x % MOD) if (y & 1) ans = 1LL * ans * x % MOD; return ans; } } inline int calc(void) { static char s1[60]; int n1 = 0; static int s2[60]; int n2 = 0; s2[1] = 0; for (char c = rdc(); c != ‘\n‘; ) if (isdigit(c)) { int x = 0; for (; isdigit(c); c = rdc()) x = x*10+c-‘0‘; s2[++n2] = x; } else { while (n1 > 0 && bond[ id[s1[n1]] ][ id[c] ] == ‘>‘) { // 前面 的 优先级 比 后面 高 s2[n2-1] = compute(s2[n2-1], s2[n2], s1[n1]); s1[n1--] = s2[n2--] = 0; } if (c == ‘)‘) s1[n1--] = 0; else s1[++n1] = c; c = rdc(); } while (n1 > 0) { s2[n2-1] = compute(s2[n2-1], s2[n2], s1[n1]); s1[n1--] = s2[n2--] = 0; } // 保证最后 n1 = 0, n2 = 1 return s2[1]; } int main(void) { id[‘^‘] = 0, id[‘*‘] = 1, id[‘+‘] = id[‘-‘] = 2, id[‘)‘] = 3, id[‘(‘] = 4; printf("%d\n", calc()); return 0; }
开一个栈存数字.
遇到一个数字的时候, 把数字压入栈中.
遇到一个运算符的时候, 把栈顶的两个数字弹出进行运算, 将新得到的数字压入栈中.
前缀表达式形如 $+~a~b$ .
中缀表达式形如 $a~+~b$ .
后缀表达式形如 $a~b~+$ .
我们猜测: 一定有一个结构, 能够统一刻画出三种表达式.
所幸的是, 我们发现了这个结构, 二叉树!
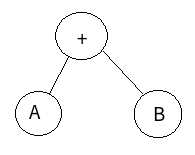
二叉树的每个节点是表达式的一个运算符或一个数字.
叶子节点是数字, 否则是运算符.
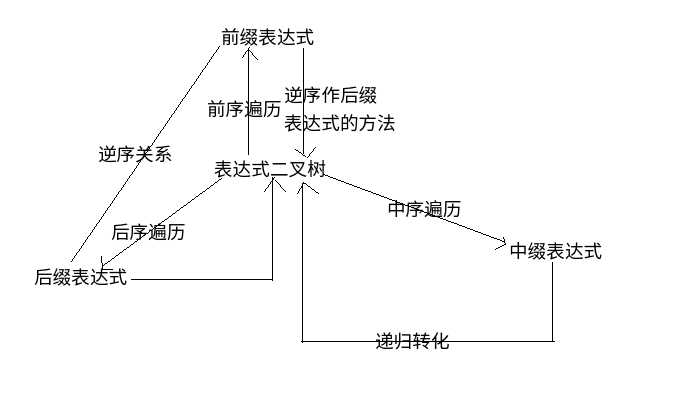
前序遍历就是前缀表达式.
中序遍历就是中缀表达式.
后序遍历就是后缀表达式.
也就是说, 如果能实现中缀表达式, 后缀表达式转二叉树, 那么就可以实现三者互化.
如果给定这么一棵二叉树, 我们也可以通过树形DP算出表达式的值.
奠基: $f_{current} = s_{current}$ .
转移: $f_{current} = compute(f_{leftson}, f_{rightson}, s_{current})$ .
答案: $f_{root}$ .
我们考虑递归建树, 定义函数 int Build(int l, int r) .
当 $s[l:r]$ 为一个数字的时候, 直接建立一个新点, 将新点上的权值赋为这个数字, 并返回这个新点.
当 $s_l$ 为左括号, $s_r$ 为右括号, 且相互匹配的时候, 返回 Build(l+1, r-1) .
否则查找 $s[l:r]$ 中优先级最小的运算符, 建立一个新点, 将这个点上的权值赋为运算符, 递归调用左边和右边, 然后返回当前点.
我们考虑维护一个栈.
遇到一个数字的时候, 就把这个数字压入栈中.
遇到一个运算符的时候, 就把栈顶的两个数字弹出, 并将他们的父亲设为这个运算符, 再将这个运算符压入.
标签:3.3 最小 定义函数 中序 inline 3.1 == har 一个栈
原文地址:http://www.cnblogs.com/Sdchr/p/7221445.html