标签：src com 指标 元素 注意 位移 .com 公式 因子
关于高斯-博内-陈
平面上任一三角形的三内角之和恒等于π,对于一般曲面上由三条测地线构成的三角形,其内角和等于π加上高斯曲率K在此三角形所围曲面上的积分.
1827年,高斯证明了这一定理.
1944年,博内将这一定理推广到一般曲面上,由任一闭曲线C围成的单连通区域,形成了著名的高斯—博内公式.
1944年,陈省身给出了高斯—博内公式的内藴证明.
欧拉数虽然神秘有趣,可还是引不起数学家们的强烈兴趣,原因是它太简单了,小学生都可以很快弄懂这些数的来源,那个时代的数学家们总是希望有个积分,微分什么的,以显示其高深莫测,高斯那时候正在研究曲面和曲线的几何学,对于各种曲率玩得和吃饭喝水似的,这个时候人们还没有意识到弯曲可以是几何的内蕴性质,而一般考虑嵌入曲率,第一个认识到弯曲可以不需要嵌入的人是黎曼.
某天,对于没有边界的二维曲面,高斯搞了一个曲率做了一个积分,他发现,他能够计算出欧拉数!很快他把这个公式推广到带边界(二维面上有洞的情形)的二维曲面, 同样得到了相应的欧拉数.
高斯当时应该是没有认识到这个公式的巨大作用,以至于他懒得去发表这样的结果,他认为这种工作对他而言太简单了,只和弟子们稍微讨论了一下,然后,就转去研究别的东西去了,可见这些宗师级的人物也有走眼的时候,几年以后,博内得到了同样的结果.
令人兴奋的是,我们导出黎曼曲率的途径,还能够让我们一瞥高斯-博内公式的风采,真正体验一番研究内蕴几何的味道.
高斯-博内公式是大范围微分几何学的一个经典的公式,它建立了空间的局部性质和整体性质之间的联系,而我们从一条几何的路径出发,结合一些矩阵变换和数学分析的内容,逐步导出了测地线、协变导数、曲率张量,现在还可以得到经典的高斯-博内公式,可见我们在这条路上已经走得足够远了,虽然过程不尽善尽美,然而,并没有脱离这个系列的核心:几何直观.
I.简单证明,如下:
首先,从
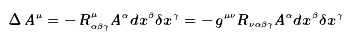
出发,交换β,γ位置,得到
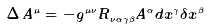
利用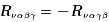
,两式相加,得到
这个式子的一般几何意义需要用外微分、曲面积分等内容诠释,我们不作讨论,但我们可以在二维空间这个特例中(即考虑三维欧式空间的二维曲面)考虑,这样,几何意义变得清晰起来,在n=2时,每个求和指标实际上只有两项求和,即
可以先算β,γ的求和,因为行列式的存在,实际上只有β≠γ时有意义,然后再利用
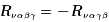
得到
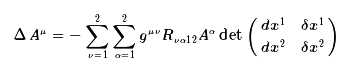
接着考虑v,a的求和,类似地也只有v≠a的时候才有意义,而且也有反对称
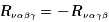
因此,可以得到
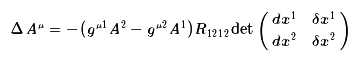
改写成
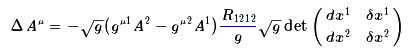
注意到,在二维空间中
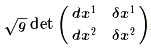
是有明确的几何意义的,它就是向量(dx1,dx2)和向量(δx1,δx2)张成的四边形的面积的结果,我们简单记为ΔS,而R1212/g正好是微分几何中定义的高斯曲率,因此,可以写成
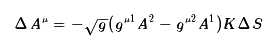
现在,我们可以分析,向量Aμ变到了Aμ+ΔAμ之后,这两个向量的夹角是多少,假设Aμ是单位向量,那么先要计算内积
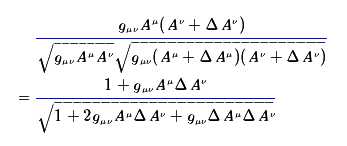
因为,cosΔθ=1-Δθ2/2+...,因此,我们要算到二阶项,即,ΔAμΔAv这一项，近似到二阶,结果为
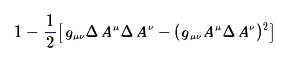
所以
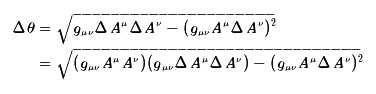
这实际上就是Aμ与ΔAμ张成的平行四边形的面积,在n=2时,也就是
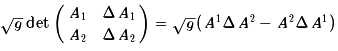
这时候,代入ΔA1,ΔA2的表达式,就得到
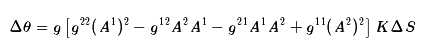
对于二阶矩阵，有一个求逆公式
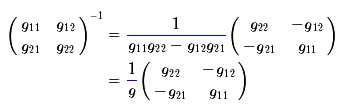
因此
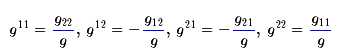
代入下式
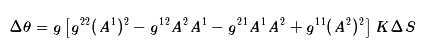
可得
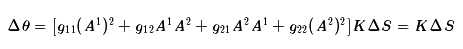
最后一个等号是因为开始就假定了Aμ是单位向量,这样,一个向量沿着小闭合曲线回来之后产生的角差,等于高斯曲率K和面元ΔS的乘积,因此,我们可以推得,如果向量沿着大范围的闭合曲线C平行移动回来,那么,变化量则表示为面积分
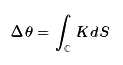
这就是微分几何中的高斯-博内公式的主要内容，即角差等于高斯曲率的面积分,诸如球面三角形的内角和等内容都与它有关,它是整体微分几何的开山之作之一
.
值得一提的是,我们上述的讨论完全是内蕴的,也就是没有引入三维空间的曲面的概念,这是很吸引人的,陈省身自己说过,他一生最好的工作就是高维高斯-博内特公式的内蕴证明,在他之前的证明是外蕴的,这里是一个形象的引导,非完整的证明.
注意到,读者可能困惑的一点是：作为体积,应该是非负的,但是如果写成矩阵行列式的形式,则有正有负,似乎存在矛盾,这在不引入外微分的前提之下,确实比较难澄清,在初等的分析范畴内,唯一的解决办法是,如果出现负体积,就直接加绝对值了.
II.详细证明,如下:
利用微分流形的向量场理论,给出高斯—博内公式的一个直接的内蕴的证明.
令R^n是偶数n维的闭可定向黎曼流形[按照上下文，这里的R^n不是代表n维欧氏空间],按照将详叙于后的方法，我们在R^n中定义一个内蕴的n阶外微分形式Ω，它当然等于R^n的不变量乘以体积元素,高斯-博内公式断言,这一微分形式在R^n上的积分等于R^n的欧拉-庞加莱示性数χ,为证明这一点，我们从流形R^n转到由R^n的单位向量构成的2n-1维流形M^(2n-1),在M^(2n-1)中我们证明Ω等于一n-1阶微分形式Ⅱ的外导数,通过定义R^n上一个带有孤立奇点的连续的单位向量场,我们得到它在M^(2n-1)中的像:n维子流形V^n,而Ω在R^n上的积分就等于V^n上同样的积分,利用斯托克斯定理证明,后者等于Ⅱ在V^n的边界上的积分,现在,V^n的边界正好对应于定义在R^n中的向量场的奇点,一个著名的定理指出它们的指标和等于χ,经过如此解释,就可以计算Ⅱ在V^n的边界上的积分,并很容易证明它等于χ.
此方法当然可以用来导出同样类型的其他公式,并可以经过适当修改,推出黎曼多面体的高斯-博内公式.
a.黎曼几何基本公式概要
令R^n是闭可定向的、偶数n=2p维、r>=4阶的微分流形,假设在R^n中定义了黎曼度量,其基本张量是g_ij,各分量假设是3阶可微的,既然我们与多重积分打交道,使用嘉当处理黎曼几何的方法看来是方便的,该方法主要使用外微分形式的理论,而不是通常的张量分析,下面出现的微分形式都是外微分形式.
按照嘉当的方法,我们对R^n的每一点P给出一组相互垂直的单位向量e_1,e_2,…,e_n,它们具有方向性,这样一组数Pe_1…e_n,称为标架(frame).
R^n在P上切向量空间中的向量v可以由P上的标架表出,于是
1.v=u_ie_i,
这里指标i从1到n,重复的指标隐含求和,由列维-齐维塔平移所定义的切向量空间无限小位移法则,给出如下形式的方程组
2.dP=w_ie_i且de_i=w_ije_j,w_ij+w_ji=0,
这里w_i,w_ij是普法夫形式,它满足以下的”结构方程”：
3.dw_i=w_jw_ji且dw_ij=-w_ikw_jk+Ω_ij,Ω_ij+Ω_ji=0.
在3中,Ω_ij是外二次微分形式,它给出了空间的曲率性质.
3中等式左边项的外导数为0,根据这一结果得到Ω_ij满足以下方程组
4.w_jΩ_ji=0且dΩ_ij-w_jkΩ_ik+w_ikΩ_jk=0,
叫做,比安基恒等式.
为了以后的计算,要了解当标架e_1…e_n作特征正交变换时,Ω_ij如何变化.
在P的一个使同一的坐标系保持有效的邻域里,令e_1…e_n通过特征正交变换变成e_1^*…e_n^*:
5.e_i^*=a_ije_j
或
5’. e_i=a_jie_j^*
这里,(a_ij)是特征正交矩阵,其元素a_ij是坐标的函数,假设Ω_ij^*由标架Pe_1^*…e_n^*形成,就如同Ω_ij由标架Pe_1…e_n形成一样,于是我们容易发现
6.Ω_ij^*=a_ika_jlΩ_kl.
由6我们直接推出下面的结果
令,εi_1…i_n是一个符号,它根据i_1,…,i_n是1,…,n的偶置换还是奇置换而取+1或-1值,其他情况下就为0.
由于我们的空间R^n是偶数维n=2p,所以可构造如下的和
7.Ω=(-1)^(p-1)[1/(2^(2p))(pi^p)(p!)]εi_1…i_2pΩi_1i_2Ωi_3i_4…Ωi_(2p-1)i_2p，
这里每一指标都从1到n.
利用6我们可以看到Ω在标架变换5下是不变的,所以它是内蕴的.
这一内蕴的微分形式是n阶的,所以它是w_1…w_n的倍数.
由于后者的乘积也是内蕴的,因此,我们可以写
8.Ω=Iw_1…w_n，
这里系数I是该黎曼流形的不变标量.
根据这些结果,我们就可以把高斯-博内公式写成如下形式
9.∫_R^nΩ=χ，
其中χ是R^n的欧拉-庞加莱特征.
b.单位向量空间与关于Ω的一个公式
现在我们要从黎曼流形R^n转到由其单位向量构成的2n-1维流形M^(2n-1).
它是r-1阶的闭微分流形,我们当然可以把R^n的局部坐标以及1中向量v的分量u_i作为M^(2n-1)的局部坐标,它们满足条件
1’.u_iu_i=1.
如果,θ_i是dv的关于标架e_1...e_n的分量,我们有
10.dv=θ_ie_i,
这里
11.θ_i=du_i+u_jw_ji,
及
12.u_iθ_i=0.
对11微分,我们得到
13.dθ_i=θ_jw_ji+u_jΩ_ji.
至于标架变换5对分量u_i,θ_i的影响,由以下方程给出
14.u_i^*=a_iju_j,θ_i^*=a_ijθ_j.
现在,我们建构以下两组微分形式:
15.Φ_k=,
16.Ψ_k=.
形式Φ_k是2p-1阶,Ψ_k是2p阶,同时,我们注意到Ψ_(p-1)与Ω只相差一个常数因子,利用6与14我们发现Φ_k和Ψ_k都是内蕴的,从而,定义在整个黎曼流形R^n上.
c.高斯-博内公式的证明
在R^n是闭的可定向黎曼流形的假设下,我们根据2、4式来给出9式的证明.
我们在R^n中定义一个在R^n的点0上有唯一奇点的连续单位向量场.
一个著名的定理指出该场在0点的指标等于R^n的欧拉-庞加莱示性数χ.
陈运用嘉当首创的外微分方法,对流形上的每一点P给出一组正交的单位切向量,成为标架,这些标架与流形本身一起组成了该流形的单位切丛,通过反映这些切向量的列维-齐维塔联络性质的方程组,得到反映空间曲率性质的一些外二次微分式,这些微分式的组合得到一个内蕴的n阶微分式Ω,证明这个Ω是单位切丛里的一个外导数,然后,利用欧拉-庞加莱-霍普夫定理,终于,证明关于Ω的积分就等于流形的欧拉-庞加莱示性数χ,这就是完成了高斯-博内公式.
千古寸心事,欧高黎嘉陈.
标签：src com 指标 元素 注意 位移 .com 公式 因子
原文地址：http://www.cnblogs.com/milantgh/p/7231354.html
