最大流

标签：搜索   nbsp   log   出队   有向图   参考   为什么   多少   遍历   

一、相关定义

【基本的网络流最大流模型】

• 一个流网络，有n个点，m条有向边；
• 源点：只出不进；（通常规定为1号点）；
• 汇点：只进不出；（通常规定为n号点）；
• 每条有向边上有两个量，容量和流量且满足“流量<=容量”，且除汇点和源点以外的点的“流入==流出”；
• 从点i到点j的容量通常用c[i,j]表示，流量则通常是f[i,j]；
• 把源点比作工厂的话，问题就是求从工厂最大可以发出多少货物，前提是不能超过道路的容量限制，也就是，最大流；
• 假如所有边上的流量都没有超过容量(不大于容量)，那么就把这一组流量，或者说，这个流，称为一个可行流。

模型如图（此图的最大流为1+2=3）：（每条有向边上便是“流量/容量”）

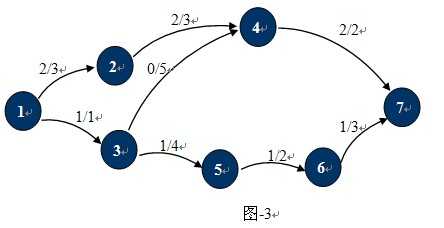
【相关定义】

有一网络流如图-4所示：

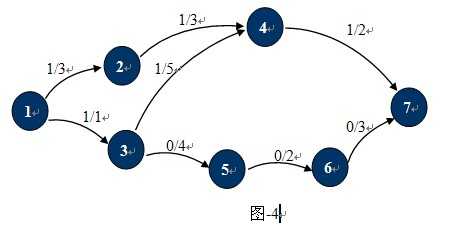
增广路径：从源节点S到汇点T的简单路径。

图-4中的增广路径有：1-2-4-7 和 1-3-4-7

图-4的残余网络如图-5所示：

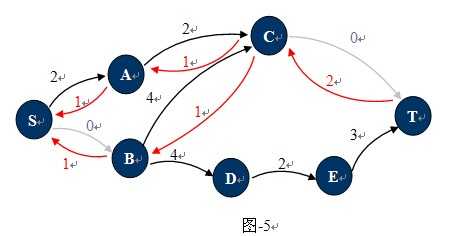
如何变成残余网络：对于已经找到一条从S 到T的路径的网络中，只要在这条路径上，把C(u,v)的值更新为C(u,v)-P(u,v)，并且添加反向弧C(v,u)。

提示：此外在未做任何操作之前，原始的有向图也是一个残余网络，它仅仅是未做任何更新而已。

残余网络：给定图G和流量f，残余网络Gf就是由那些仍有空间对流量进行增加的边构成。在流网络中, 若某条边的流量小于其容量, 则将其加入的Gf中；若某条边流量等于其容量，则这条边将不属于Gf（看图-5，有两条这样的边已被标记成灰的，即不属于残余网络）。

增广路径：残存网络Gf中一条从源节点S到汇点T的简单路径。

最大流定理：如果残留网络上找不到增广路径，则当前流为最大流；反之，如果当前流不为最大流，则一定有增广路径。

二、算法实现

Ford-Fulkerson方法

介绍完上面的概念之后，便可以用Ford-Fulkerson方法求最大流了。为什么叫Ford-Fulkerson方法而不是算法，原因在于可以用多种方式实现这一方法，方式并不唯一。

下面介绍一种基于广度优先搜索(BFS)来计算增广路径P的算法：Edmonds-Karp算法。

算法流程如下：

  设队列Q：存储当前未访问的节点，队首节点出队后，成为已检查的标点；

  Path数组：存储当前已访问过的节点的增广路径；

  Flow数组：存储一次BFS遍历之后流的可改进量；

  Repeat:

    Path清空；

    源点S进入Path和Q，Path[S]<-0，Flow[S]<-+∞；

    While Q非空 and 汇点T未访问 do

        Begin

            队首顶点u出对；

            For每一条从u出发的弧(u,v) do

                If v未访问 and 弧(u,v) 的流量可改进；

                Then Flow[v]<-min(Flow[u],c[u][v]) and v入队 and Path[v]<-u；

    End while

   

    If(汇点T已访问)

    Then 从汇点T沿着Path构造残余网络；

  Until 汇点T未被访问

三、沙场练兵

题目一、http://poj.org/problem?id=1273

题解：http://www.cnblogs.com/kuangbin/archive/2011/07/26/2117636.html

四、参考资料

博客：最大流 — Edmond Karp算法

博客：http://blog.csdn.net/yiqingnian28/article/details/23388633

博客：http://www.cnblogs.com/kuangbin/archive/2011/07/26/2117636.html

最大流

标签：搜索   nbsp   log   出队   有向图   参考   为什么   多少   遍历   

原文地址：http://www.cnblogs.com/xzxl/p/7236154.html