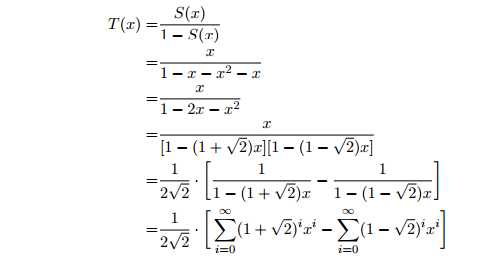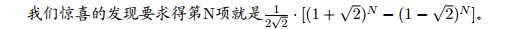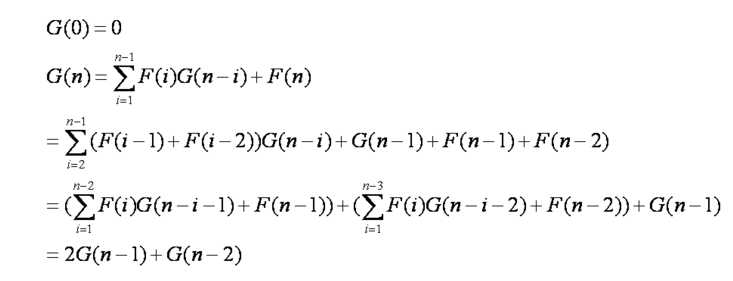lqp在为出题而烦恼,他完全没有头绪,好烦啊… 他首先想到了整数拆分。整数拆分是个很有趣的问题。给你一个正整数N,对于N的一个整数拆分就是满足任意m>0,a1 ,a2 ,a3…am>0,且a1+a2+a3+…+am=N的一个有序集合。通过长时间的研究我们发现了计算对于N的整数拆分的总数有一个很简单的递推式,但是因为这个递推式实在太简单了,如果出这样的题目,大家会对比赛毫无兴趣的。然后lqp又想到了斐波那契数。定义F0=0,F1=1,Fn=Fn-1+Fn-2 (n>1),Fn就是斐波那契数的第n项。但是求出第n项斐波那契数似乎也不怎么困难… lqp为了增加选手们比赛的欲望,于是绞尽脑汁,想出了一个有趣的整数拆分,我们暂且叫它:整数的lqp拆分。和一般的整数拆分一样,整数的lqp拆分是满足任意m>0,a1 ,a2 ,a3…am>0,且a1+a2+a3+…+am=N的一个有序集合。但是整数的lqp拆分要求的不是拆分总数,相对更加困难一些。对于每个拆分,lqp定义这个拆分的权值Fa1Fa2…Fam,他想知道对于所有的拆分,他们的权值之和是多少?简单来说,就是求 由于这个数会十分大,lqp稍稍简化了一下题目,只要输出对于N的整数lqp拆分的权值和mod 109(10的9次方)+7输出即可。
输出一个整数,为对于N的整数lqp拆分的权值和mod 109(10的9次方)+7。
20%数据满足:1≤N≤25 50%数据满足:1≤N≤1000 100%数据满足:1≤N≤1000000
给出两种解法
1.

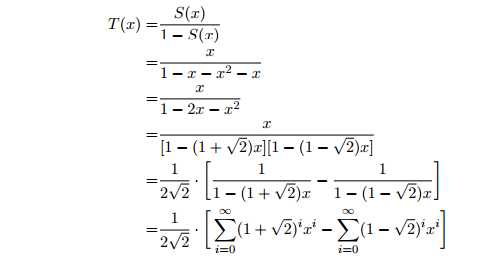
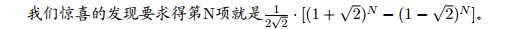

母函数还不知道,先当逆元和组合数练习题
1 #include<iostream>
2 #include<cstdio>
3 #include<algorithm>
4 #include<cstring>
5 using namespace std;
6 typedef long long lol;
7 int Mod=1000000007;
8 lol ans,A[1000001],c[1000001];
9 int n;
10 lol pow(lol x,int y)
11 {
12 lol res=1;
13 while (y)
14 {
15 if (y%2==1) res=(res*x)%Mod;
16 x=(x*x)%Mod;
17 y=y/2;
18 }
19 return res;
20 }
21 int main()
22 {int i;
23 cin>>n;
24 A[1]=1;
25 for (i=2;i<=n;i++)
26 A[i]=((Mod-Mod/i)*A[Mod%i])%Mod;
27 c[1]=n;
28 ans=(ans+n)%Mod;
29 for (i=1;i<=(n-1)/2;i++)
30 {
31 c[2*i+1]=(((c[2*i-1]*(n-2*i))%Mod)*(n-2*i+1)%Mod)%Mod;
32 c[2*i+1]=(((c[2*i+1]*A[2*i])%Mod)*A[2*i+1])%Mod;
33 ans=(ans+(c[2*i+1]*pow(2,i))%Mod)%Mod;
34 }
35 cout<<ans;
36 }
2.打表找规律:
G[n]=2G[n-1]+G[n-2],G[0]=0,G[1]=1
不过可以通过40分dp推导
暴力显然有G[n]=ΣG[i]*F[n-i]+F[n],O(n^2)
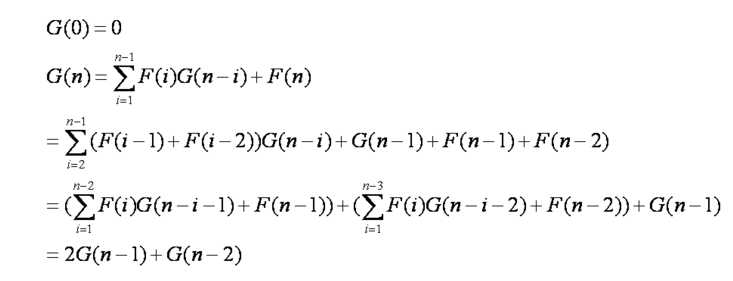
1 #include<cstdio>
2 int n;long long mod=1e9+7,g[1000010];
3 int main()
4 {
5 scanf("%d",&n);g[1]=1;
6 for(int i=2;i<=n;i++)g[i]=(2*g[i-1]+g[i-2])%mod;
7 printf("%lld\n",g[n]);
8 }