欧拉函数

标签：数值   width   ddl   分解   stat   无法   部分   简单   情况   

欧拉函数是小于n的正整数中与n互质的数的数目（φ(1)=1）

啊啊证明不会

另外偶拉函数是积性函数

啊啊但是公式背过了

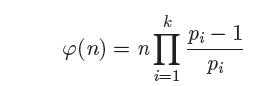
那么

代码吧，我的理解，ret为

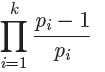
该部分求出后，分数为n时的分子，（我们设qwq=n）那么，把分母变大的过程转化为n的减小，同时分子变大，当n不能分解时表示 分母*n=qwq，此时分子就是该数的欧拉函数值

是不是特别简单

但要考虑一个质因数出现多次情况，此时如果n只除一次该质因数，则无法化为最简，多以多次除，那么分子（第一次要*（改质因数-1））也要乘该质因数

啊啊啊啊，就这么水过去了

复杂度么（O(sqrt(n)）的啦

int getphi(int x){
    int ret=1;
    for(int i=1;prime[i]*prime[i]<=x;i++){
        if(x%prime[i]==0)
        {
            ret*=prime[i]-1;
            x/=prime[i];
            while(x%prime[i]==0)
            x/=prime[i],ret*=prime[i];
        }
    }
    if(x>1) ret*=x-1;
    return ret;
}

欧拉函数

标签：数值   width   ddl   分解   stat   无法   部分   简单   情况   

原文地址：http://www.cnblogs.com/sssy/p/7241596.html