标签:work 比较 models auto 思想 技术 好处 额外 概率
本章我们介绍词的向量表征,也称为word embedding。词向量是自然语言处理中常见的一个操作,是搜索引擎、广告系统、推荐系统等互联网服务背后常见的基础技术。
在这些互联网服务里,我们经常要比较两个词或者两段文本之间的相关性。为了做这样的比较,我们往往先要把词表示成计算机适合处理的方式。最自然的方式恐怕莫过于向量空间模型(vector space model)。 在这种方式里,每个词被表示成一个实数向量(one-hot vector),其长度为字典大小,每个维度对应一个字典里的每个词,除了这个词对应维度上的值是1,其他元素都是0。
One-hot vector虽然自然,但是用处有限。比如,在互联网广告系统里,如果用户输入的query是“母亲节”,而有一个广告的关键词是“康乃馨”。虽然按照常理,我们知道这两个词之间是有联系的——母亲节通常应该送给母亲一束康乃馨;但是这两个词对应的one-hot vectors之间的距离度量,无论是欧氏距离还是余弦相似度(cosine similarity),由于其向量正交,都认为这两个词毫无相关性。 得出这种与我们相悖的结论的根本原因是:每个词本身的信息量都太小。所以,仅仅给定两个词,不足以让我们准确判别它们是否相关。要想精确计算相关性,我们还需要更多的信息——从大量数据里通过机器学习方法归纳出来的知识。
在机器学习领域里,各种“知识”被各种模型表示,词向量模型(word embedding model)就是其中的一类。通过词向量模型可将一个 one-hot vector映射到一个维度更低的实数向量(embedding vector),如embedding(母亲节)=[0.3,4.2,?1.5,…],embedding(康乃馨)=[0.2,5.6,?2.3,…] 。在这个映射到的实数向量表示中,希望两个语义(或用法)上相似的词对应的词向量“更像”,这样如“母亲节”和“康乃馨”的对应词向量的余弦相似度就不再为零了。
词向量模型可以是概率模型、共生矩阵(co-occurrence matrix)模型或神经元网络模型。在用神经网络求词向量之前,传统做法是统计一个词语的共生矩阵X。X是一个|V|×|V| 大小的矩阵,Xij表示在所有语料中,词汇表V(vocabulary)中第i个词和第j个词同时出现的词数,|V|为词汇表的大小。对X做矩阵分解(如奇异值分解,Singular Value Decomposition [5]),得到的U即视为所有词的词向量:
$X=USV^T$
但这样的传统做法有很多问题:
1) 由于很多词没有出现,导致矩阵极其稀疏,因此需要对词频做额外处理来达到好的矩阵分解效果;
2) 矩阵非常大,维度太高(通常达到106?106的数量级);
3) 需要手动去掉停用词(如although, a,…),不然这些频繁出现的词也会影响矩阵分解的效果。
基于神经网络的模型不需要计算存储一个在全语料上统计的大表,而是通过学习语义信息得到词向量,因此能很好地解决以上问题。在本章里,我们将展示基于神经网络训练词向量的细节,以及如何用PaddlePaddle训练一个词向量模型。
在这里我们介绍三个训练词向量的模型:N-gram模型,CBOW模型和Skip-gram模型,它们的中心思想都是通过上下文得到一个词出现的概率。对于N-gram模型,我们会先介绍语言模型的概念,并在之后的训练模型中,带大家用PaddlePaddle实现它。而后两个模型,是近年来最有名的神经元词向量模型,由 Tomas Mikolov 在Google 研发[3],虽然它们很浅很简单,但训练效果很好。
语言模型
在介绍词向量模型之前,我们先来引入一个概念:语言模型。 语言模型旨在为语句的联合概率函数P(w1,…,wT)建模, 其中wi表示句子中的第i个词。语言模型的目标是,希望模型对有意义的句子赋予大概率,对没意义的句子赋予小概率。 这样的模型可以应用于很多领域,如机器翻译、语音识别、信息检索、词性标注、手写识别等,它们都希望能得到一个连续序列的概率。 以信息检索为例,当你在搜索“how long is a football bame”时(bame是一个医学名词),搜索引擎会提示你是否希望搜索”how long is a football game”, 这是因为根据语言模型计算出“how long is a football bame”的概率很低,而与bame近似的,可能引起错误的词中,game会使该句生成的概率最大。
对语言模型的目标概率P(w1,…,wT),如果假设文本中每个词都是相互独立的,则整句话的联合概率可以表示为其中所有词语条件概率的乘积,即:
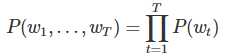
然而我们知道语句中的每个词出现的概率都与其前面的词紧密相关, 所以实际上通常用条件概率表示语言模型:
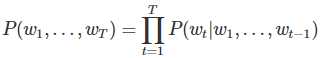
在计算语言学中,n-gram是一种重要的文本表示方法,表示一个文本中连续的n个项。基于具体的应用场景,每一项可以是一个字母、单词或者音节。 n-gram模型也是统计语言模型中的一种重要方法,用n-gram训练语言模型时,一般用每个n-gram的历史n-1个词语组成的内容来预测第n个词。
Yoshua Bengio等科学家就于2003年在著名论文 Neural Probabilistic Language Models [1] 中介绍如何学习一个神经元网络表示的词向量模型。文中的神经概率语言模型(Neural Network Language Model,NNLM)通过一个线性映射和一个非线性隐层连接,同时学习了语言模型和词向量,即通过学习大量语料得到词语的向量表达,通过这些向量得到整个句子的概率。用这种方法学习语言模型可以克服维度灾难(curse of dimensionality),即训练和测试数据不同导致的模型不准。注意:由于“神经概率语言模型”说法较为泛泛,我们在这里不用其NNLM的本名,考虑到其具体做法,本文中称该模型为N-gram neural model。
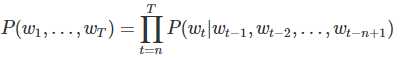
给定一些真实语料,这些语料中都是有意义的句子,N-gram模型的优化目标则是最大化目标函数:
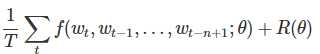
其中f(wt,wt?1,…,wt?n+1)表示根据历史n-1个词得到当前词$w_t$的条件概率,R(θ)表示参数正则项。
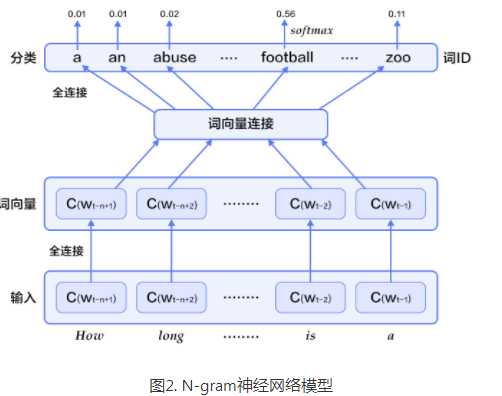
图2展示了N-gram神经网络模型,从下往上看,该模型分为以下几个部分:
1.对于每个样本,模型输入wt?n+1,…wt?1, 输出句子第t个词为字典中|V|个词的概率。每个输入词wt?n+1,…wt?1首先通过映射矩阵映射到词向量C(wt?n+1),…C(wt?1)。
2.然后所有词语的词向量连接成一个大向量,并经过一个非线性映射得到历史词语的隐层表示:
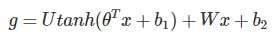
其中,x为所有词语的词向量连接成的大向量,表示文本历史特征;θ、U、b1、b2和W分别为词向量层到隐层连接的参数。g表示未经归一化的所有输出单词概率,gi表示未经归一化的字典中第i个单词的输出概率。
3.根据softmax的定义,通过归一化gi, 生成目标词wt的概率为:
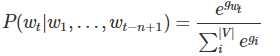
4.整个网络的损失值(cost)为多类分类交叉熵,用公式表示为
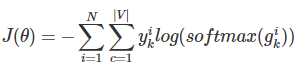
其中$y^i_k$表示第i个样本第k类的真实标签(0或1),softmax(gik)表示第i个样本第k类softmax输出的概率。
CBOW模型通过一个词的上下文(各N个词)预测当前词。当N=2时,模型如下图所示:
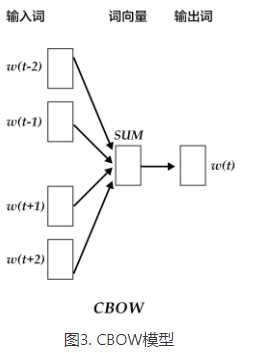
具体来说,不考虑上下文的词语输入顺序,CBOW是用上下文词语的词向量的均值来预测当前词。即:
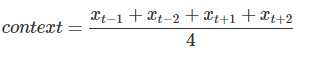
其中xt为第t个词的词向量,分类分数(score)向量 z=U?context,最终的分类y采用softmax,损失函数采用多类分类交叉熵。
CBOW的好处是对上下文词语的分布在词向量上进行了平滑,去掉了噪声,因此在小数据集上很有效。而Skip-gram的方法中,用一个词预测其上下文,得到了当前词上下文的很多样本,因此可用于更大的数据集。
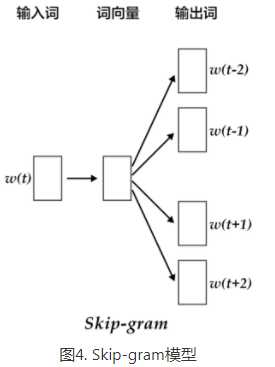
如上图所示,Skip-gram模型的具体做法是,将一个词的词向量映射到2n个词的词向量(2n表示当前输入词的前后各n个词),然后分别通过softmax得到这2n个词的分类损失值之和。
http://book.paddlepaddle.org/index.cn.html
https://www.zhihu.com/question/38102762
http://lamda.nju.edu.cn/weixs/project/CNNTricks/CNNTricks.html
标签:work 比较 models auto 思想 技术 好处 额外 概率
原文地址:http://www.cnblogs.com/ljygoodgoodstudydaydayup/p/7241791.html