标签:概念 斐波那契 证明 nec type 插入 date bre auto
AVL树是一种平衡二叉搜索树,在渐进意义下,可以保证树的高度为logn,查找、插入和删除操作均可以在O(logn)时间内完成。AVL树的名字来源,是提出它的人0 0
引入平衡因子的概念,任一节点的平衡因子定义为其左右子树的高度差。
AVL树的限定,是任何一个节点的平衡因子绝对值不大于1。可以通过继承BST来得到AVL树,只需要重写节点的插入和删除操作即可。可以证明,AVL树最少节点数为fib(h+3)-1,此时的树称为斐波那契AVL树。
1 #include"BST.h" 2 template<typename T> class AVL :public BST<T> 3 { 4 public: 5 BinNodePosi(T) insert(const T& e) override; 6 bool remove(const T& e) override; 7 };
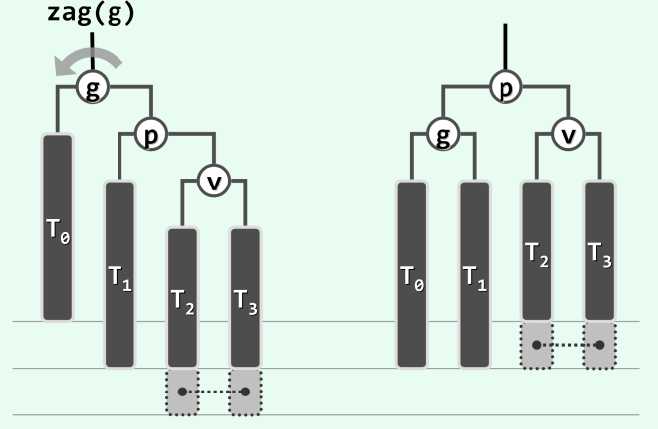
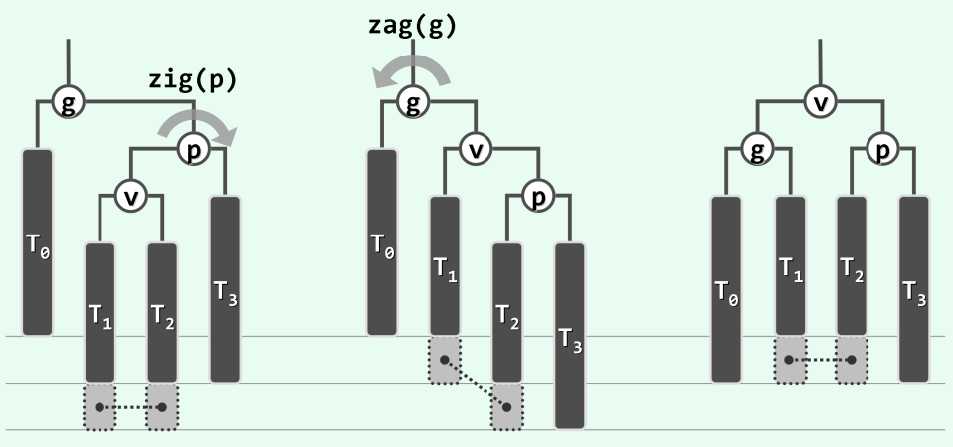
节点的插入操作,总体与BST相同,不同之处在于,如果插入后原树不满足AVL树的条件,需要进行旋转操作,重新平衡。旋转重平衡可以分为单旋和双旋,如下图所示。可以发现,旋转后以g为根的子树高度-1.
1 template<typename T> BinNodePosi(T) AVL<T>::insert(const T& e)//O(logn) 2 { 3 //std::cout << "haha" << std:: endl; 4 BinNodePosi(T)& x = search(e); if (x) return x; 5 BinNodePosi(T) xx = x = new BinNode<T>(e, _hot); _size++;//此时x的父亲_hot若增高,则祖父有可能失衡 6 for (BinNodePosi(T) g = _hot; g; g = g->parent)//从_hot检查是否失衡,用3+4算法回复 7 { 8 if (!AvlBalanced(*g)) 9 { 10 FromParentTo(*g) = rotateAt(tallerChild(tallerChild(g))); break;//并将子树重新接入原树 11 }//旋转的输入参数为g较高的孙子 12 else 13 updateHeight(g);//更新高度,即使未失衡也可能高度增加 14 } 15 //std::cout << "xixi" << std::endl; 16 return xx;//返回新节点的位置 17 }
rotateAt()在后面实现。可以证明,插入操作一旦造成一个节点失去平衡,那么其父亲也有可能失去平衡。不过,如果其父亲未失去平衡,那么更高的祖先可以不必检查,必然未失衡。因此,循环可以考虑改进,一旦一个节点失衡而某一个祖先未失衡,算法可以停止。重平衡的操作有两种情况,单旋或者双旋可以使得AVL树重新平衡。
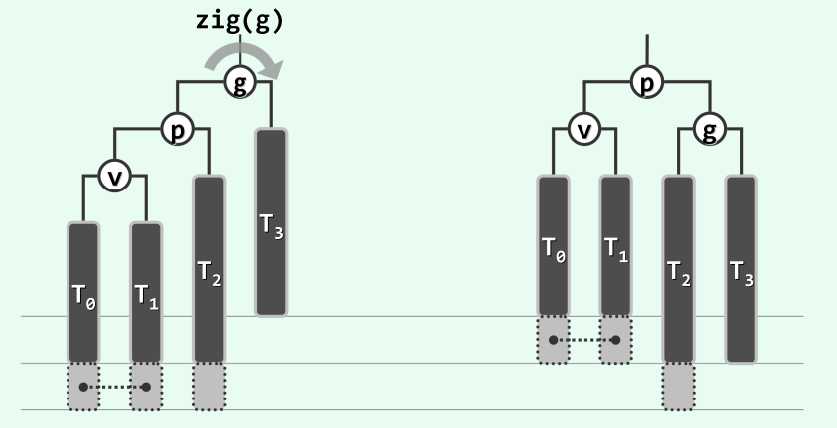
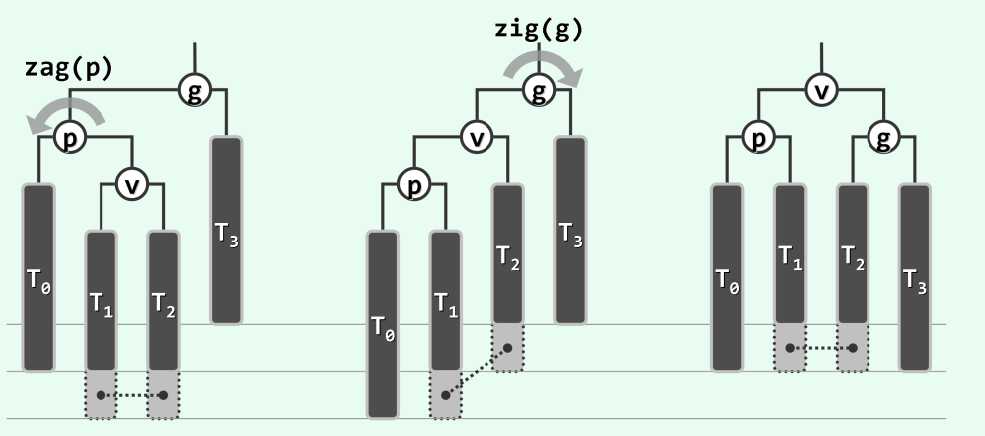
节点的删除操作,流程上类似。不过,删除操作每次只会导致一个节点失衡。可以发现,重新平衡后,以p为根的子树高度可能会降低也可能保持不变。因此,对这个节点进行旋转恢复平衡,可能会导致更高层的节点失衡,这种现象称为失衡传播。因此,需要从下到上检查节点才能保证恢复平衡。
1 template<typename T> bool AVL<T>::remove(const T& e)//O(logn) 2 { 3 BinNodePosi(T)& x = search(e); if (!x) return false; 4 removeAt(x, _hot); _size--; 5 for (BinNodePosi(T) g = _hot; g; g = g->parent)//从_hot开始向上检查,可能造成失衡传播 6 { 7 if (!AvlBalanced(*g)) 8 g = FromParentTo(*g) = rotateAt(tallerChild(tallerChild(g))); //原父亲 9 updateHeight(g);//更新高度,即使未失衡也可能高度增加 10 }//最坏情况需要做O(logn)次 11 return true;//返回新节点的位置 12 }
最后,实现重新恢复平衡的方法。其实,综合以上的单旋和双旋情况,可以综合为一个统一的问题,即三个节点和四棵子树的重新组合,具体如下图:
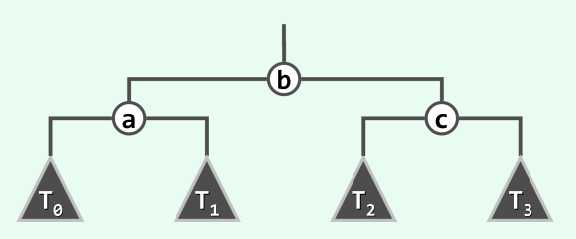
因此,可以把插入和删除的单双旋操作统一纳入到框架中,分情况连接这三个节点和四棵子树:
1 template<typename T> BinNodePosi(T) BST<T>::connect34(BinNodePosi(T) a, BinNodePosi(T) b, BinNodePosi(T) c, 2 BinNodePosi(T) T0, BinNodePosi(T) T1, BinNodePosi(T) T2, BinNodePosi(T) T3) 3 { 4 a->lc = T0; if (T0) T0->parent = a; 5 a->rc = T1; if (T1) T1->parent = a; updateHeight(a); 6 c->lc = T2; if (T2) T2->parent = c; 7 c->rc = T3; if (T3) T3->parent = c; updateHeight(c); 8 b->lc = a; a->parent = b; 9 b->rc = c; c->parent = b; updateHeight(b); 10 return b;//返回新树的根节点 11 } 12 template<typename T> BinNodePosi(T) BST<T>::rotateAt(BinNodePosi(T) v) 13 { 14 BinNodePosi(T) p = v->parent; BinNodePosi(T) g = p->parent;//根据v,p,g相对位置分四种情况 15 if(IsLChild(*p))//zig,p是左孩子 16 if (IsLChild(*v))//zig-zig 17 { 18 p->parent = g->parent; 19 return connect34(v, p, g, v->lc, v->rc, p->rc, g->rc); 20 } 21 else //zig-zag 22 { 23 v->parent = g->parent; 24 return connect34(p, v, g, p->lc, v->lc, v->rc, g->rc); 25 } 26 else//zag,p是右孩子 27 if (IsRChild(*v)) 28 { 29 p->parent = g->parent; 30 return connect34(g, p, v, g->lc, p->lc, v->lc, v->rc); 31 } 32 else 33 { 34 v->parent = g->parent; 35 return connect34(g, v, p, g->lc, v->lc, v->rc, p->rc); 36
标签:概念 斐波那契 证明 nec type 插入 date bre auto
原文地址:http://www.cnblogs.com/lustar/p/7219861.html