标签：整理   结束   最大   log   出发点   font   参考   table   round   

     问题定义     

流网络

• 图G=(V,E)：有向图、连通图
• 容量：每条边(u, v)∈G有非负的容量值c(u, v)，表示该边的流量最大值
• 反平行边：两条边的起点和终点相反，(u, v)和(v, u)是反平行
  • 图中不允许有反平行边，也就是有边(u, v)，则不存在反方向的边(v, u)
  • 图中不允许自循环
• 图中有两个点源结点s和汇点t。源结点是网络流的起点，汇点是流的终点

 G中流

• 一个实值函数f：V x V -> R，两个点间的流量

• 性质1——容量限制：每条边上的流不超过容量。对于所有结点u, v∈V，要求0≤f(u, v)≤c(u v)

• 性质2——流量守恒：除了源结点和汇点，每个点的流入量=流出量

最大流问题

给定一个流网络G、一个源结点s、一个汇点t，找到值最大的一个流

定义：出发点为源点，接受流量 的汇聚点为汇点，边上的权值为可以流过的最大值

     几个关键定义     

残存网络G_f：由仍可以对流量进行增加/减少的边构成（流过的量不超过容量的边），包含原图中的边，以及可能包含对应的反向边

残存容量c_{f：一条边还可以增加的最大流量（与容量c不同，c表示的是一开始就确定的流量最大值）}

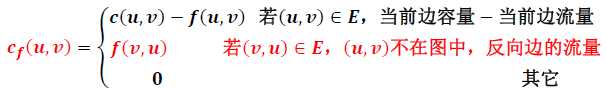
由c_f再定义一次G_f：c_f>0的边

为什么要在G_f中加反向边？

通过增加反向边，让我们可以撤销原来的流量操作。为什么要撤销呢？

来自《数据结构与算法分析》上的一个例子

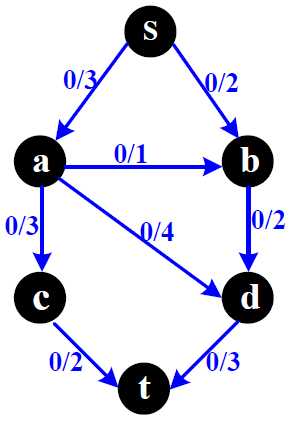
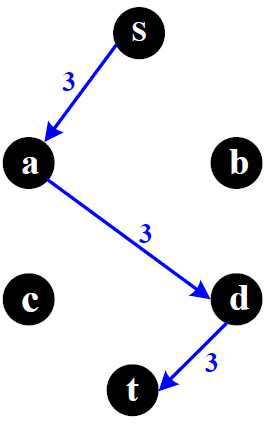
原图	流图（原图上的流）	残余网络
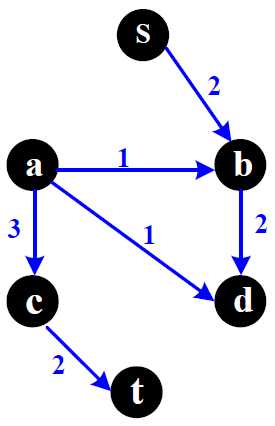			残余网络中没有增加反向边 s->t没有新的可达路径 算法结束，但没有达到目的 （得到最大流）
原来的网络流图 0/5表示边的容量为5	图中每条边上流量的一个状态 选择一条可达路径s-a-d-t 发送流量=3到这条路径上		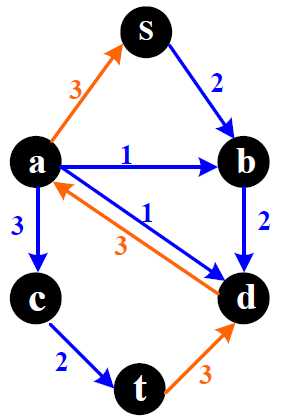增加了反向边， s->t存在新的可达路径 把原来s-a-d-t的流撤销一部分 被撤销的部分可以分流到其它路径

增广路径：给定流网络G=(V, E)，增广路径是残存网络中一条从源结点到汇点的简单路径（没有分支）

流网络的切割

流网络G=(V, E)的一个切割就是将结点集合划分成两个集合S和T（T=V-S）

• 切割(S, T)的容量：集合S中每个点到集合T中每个点的容量之和

• 最小切割：网络中容量最小的切割
• 最大流最小切割定理

设f为流网络G=(V, E)中的一个流，该流网络的源结点为s，汇点为t，则下面的条件等价：

• • f是G的一个最大流
  • 残存网络G_f不包括任何增广路径
  • |f|=c(S, T) 流网络中任意流都不能超过任意切割的容量

     Ford-Fulkerson方法     

基本步骤

1. 寻找一条增广路径p，用p来对流进行修改（增加）
2. 直到没有任何增广路径

整理了一下概念，接下来找找例子再补一下

参考

1. 《算法导论》原书第3版

2. 《数据算法与算法分析——C语言描述》原书第2版

最大网络流

标签：整理   结束   最大   log   出发点   font   参考   table   round   

原文地址：http://www.cnblogs.com/coolqiyu/p/7251643.html