RANSAC

标签：null   技术   应用   amp   存在   --   数据   数据集   选择   

一、概述

RANSAC(RANdom SAmple Consensus)随机抽样一致，是用来从一组观测数据中估计数学模型参数的一种方法。由于是观测数据，避免不了有误差存在，当误差太大了就变成了无效数据outlier（与outlier对应的是inlier有效数据）。如果我们在估计参数的时候没有剔除掉这些无效的数据，结果会被这些无效数据所影响。所以我们希望采用一种方法从数据集的inliers中估计模型参数，这就是RANSAC.

二、算法描述

1.  输入

• 数据------------------------------------一组观测数据
• 模型------------------------------------含有参数的模型
• 确定模型参数的最小数据个数n---例如确定一条直线至少要两个点
• 最大迭代次数k-----------------------最大迭代次数
• 误差阈值t-----------------------------误差在阈值t之内，则认为是有效数据
• 符合模型数据的个数d--------------如果数据中有d个数据符合迭代中产生的模型，则认为该模型有效，即可以认为该模型包含足够都的有效数据

2. 输出

• 模型参数（成功找到合适的模型）或NULL（没有找到合适的参数）

3. 步骤

• 从数据中随机挑选n个数据，假设这n个数据都是有效的（只是算法认为其有效，并非真正有效），用这个n个数据求出模型参数（例如用解方程组的方法）
• 用第一步生成的模型依次验证剩下的数据，统计在误差阈值t之内的数据个数c，如果c>d，认为该模型有效，否则认为该模型无效，转第一步
• 把第一步n个数据和第二步c个数据合并，检测该模型对这些数据的拟合程度，即检查该模型参数基于有效数据的好坏程度，如果比当前最好的参数好，则更换最好参数为当前参数
• 增加迭代次数，返回第一步

4. 具体描述

iterations = 0
bestfit = null
besterr = something really large
while iterations < k {
    maybeinliers = n randomly selected values from data
    maybemodel = model parameters fitted to maybeinliers
    alsoinliers = empty set
    for every point in data not in maybeinliers {
        if point fits maybemodel with an error smaller than t
             add point to alsoinliers
    }
    if the number of elements in alsoinliers is > d {
        //this implies that we may have found a good model
        // now test how good it is
        bettermodel = model parameters fitted to all points in maybeinliers and alsoinliers
        thiserr = a measure of how well model fits these points
        if thiserr < besterr {
            bestfit = bettermodel
            besterr = thiserr
        }
    }
    increment iterations
}
return bestfit

三、举例

譬如现在有一组测量的二维点数据，分布如下：

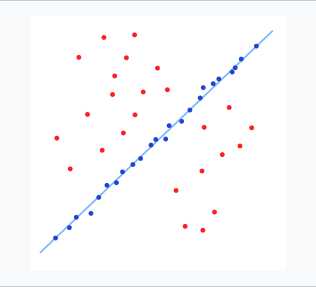
图中红色点为无效数据，蓝色点为有效数据，我们期望拟合出一条如上图的直线，然而不排除这些无效数据的话，直接采用最小二乘法会的到如下一条直线：

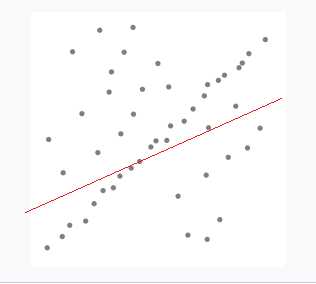
 假设共有50个点，按照RANSANC的思路：

• 从50个点随机选两个点确定一条直线L
• 基于L验证剩下的48个点中误差在t之内的数据个数，记为inlierNum，如果inlierNum < d，则表示这条直线不够好，返回第一步
• 计算第一步中的两个点和第二步中的inlierNum个点对与该直线L的残差平方和thiserr,如果thiserr<besterr，则设这个参数为最优，否则丢弃
• 继续迭代

四、参数确定

注意上面的输入数据中，除了数据和模型之外还有一些参数，那这些参数怎么确定呢？

 通常n的值由模型确定，t和d的值有观测数据和具体应用共同由实验确定。而k的值可以从理论上进行确定，直观上来讲k值越大求得最优参数的概率就越大。假设算法迭代k次能在初始选择数据时选择的都是有效数据的概率为p，数据集中有效数据的比率为w(w = 有效数据数/总数据数)，w一般是不知道的，但可以估计的偏小一点，让算法更鲁棒。n次都选择为有效数据的概率为w^n，至少有一次选择到了无效数据的概率为1-w^n，连续k次每次都至少有一次选择到了无效数据的概率为(1-w^n)^k。

有：1-p = (1-w^n)^k

则：k = log(1-p)/log(1-w^n)

假设设定p = 0.98则就能确定k=log(0.02)/log(1-w^n).通常这样确定的k要比k的实际上界偏小一点，因为上面的计算每次选择一个数据都是基于全部数据选择的，即有放回的选取，实际上不能这样，选择的时候要求数据不能重复出现。故还要在k的基础上加上一个额外值：

SD(k) = [(1-w^n)^1/2]/w^n

即实际上：k = log(1-p)/log(1-w^n)  + [(1-w^n)^1/2]/w^n.

RANSAC

标签：null   技术   应用   amp   存在   --   数据   数据集   选择   

原文地址：http://www.cnblogs.com/yhl0414/p/7256336.html