标签:owb sig algorithm queue ring fabs signed com 输入
题意:已知N*N的矩阵A,输出矩阵A + A2 + A3 + . . . + Ak,每个元素只输出最后一个数字。
分析:
A + A2 + A3 + . . . + An可整理为下式,
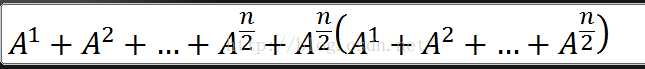
从而可以用log2(n)的复杂度算出结果。
注意:输入时把矩阵A的每个元素对10取余,因为若不处理,会导致k为1的时候结果出错。
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<cmath>
#include<iostream>
#include<sstream>
#include<iterator>
#include<algorithm>
#include<string>
#include<vector>
#include<set>
#include<map>
#include<stack>
#include<deque>
#include<queue>
#include<list>
#define lowbit(x) (x & (-x))
const double eps = 1e-8;
inline int dcmp(double a, double b){
if(fabs(a - b) < eps) return 0;
return a > b ? 1 : -1;
}
typedef long long LL;
typedef unsigned long long ULL;
const int INT_INF = 0x3f3f3f3f;
const int INT_M_INF = 0x7f7f7f7f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const LL LL_M_INF = 0x7f7f7f7f7f7f7f7f;
const int dr[] = {0, 0, -1, 1, -1, -1, 1, 1};
const int dc[] = {-1, 1, 0, 0, -1, 1, -1, 1};
const int MOD = 10;
const double pi = acos(-1.0);
const int MAXN = 40 + 10;
const int MAXT = 10000 + 10;
using namespace std;
int n;
struct Matrix{
int r, c, matrix[MAXN][MAXN];
Matrix(int rr, int cc):r(rr), c(cc){
memset(matrix, 0, sizeof matrix);
}
};
Matrix add(Matrix a, Matrix b){
Matrix ans(n, n);
for(int i = 0; i < a.r; ++i){
for(int j = 0; j < a.c; ++j){
ans.matrix[i][j] = ((a.matrix[i][j] % MOD) + (b.matrix[i][j] % MOD)) % MOD;
}
}
return ans;
}
Matrix mul(Matrix a, Matrix b){
Matrix ans(a.r, b.c);
for(int i = 0; i < a.r; ++i){
for(int j = 0; j < b.c; ++j){
for(int k = 0; k < a.c; ++k){
(ans.matrix[i][j] += ((a.matrix[i][k] % MOD) * (b.matrix[k][j] % MOD)) % MOD) %= MOD;
}
}
}
return ans;
}
Matrix QPOW(Matrix a, int k){
Matrix ans(n, n);
for(int i = 0; i < n; ++i){
ans.matrix[i][i] = 1;
}
while(k){
if(k & 1) ans = mul(ans, a);
a = mul(a, a);
k >>= 1;
}
return ans;
}
Matrix solve(Matrix tmp, int k){
if(k == 1) return tmp;
Matrix t = solve(tmp, k >> 1);
Matrix ans = add(t, mul(QPOW(tmp, k >> 1), t));
if(k & 1) ans = add(ans, QPOW(tmp, k));
return ans;
}
int main(){
int k;
while(scanf("%d%d", &n, &k) == 2){
if(n == 0) return 0;
Matrix tmp(n, n);
for(int i = 0; i < n; ++i){
for(int j = 0; j < n; ++j){
scanf("%d", &tmp.matrix[i][j]);
tmp.matrix[i][j] %= MOD;
}
}
Matrix ans = solve(tmp, k);
for(int i = 0; i < ans.r; ++i){
for(int j = 0; j < ans.c; ++j){
if(j) printf(" ");
printf("%d", ans.matrix[i][j]);
}
printf("\n");
}
printf("\n");
}
return 0;
}
UVA - 11149 Power of Matrix(矩阵倍增)
标签:owb sig algorithm queue ring fabs signed com 输入
原文地址:http://www.cnblogs.com/tyty-Somnuspoppy/p/7260766.html