标签:访问 不同 第一个 矩阵 部分 str 执行 线性 逻辑
1、无向图:边没有方向的图称为无向图。如<A,B>和<B,A>等价。下图是一个无向图,及其邻接链表和邻接矩阵的表示。
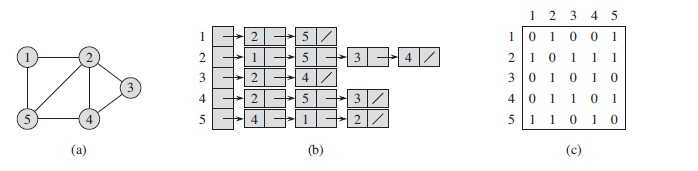
2、有向图: 边是有方向性的,例如一条边有两个顶点A,B,A和B顶点之间,A指向了B,B也指向了A,两者是不同的,如果给边赋予权重,那么这种异同便更加显著了。下图是一个有向图,及其邻接链表和邻接矩阵的表示。
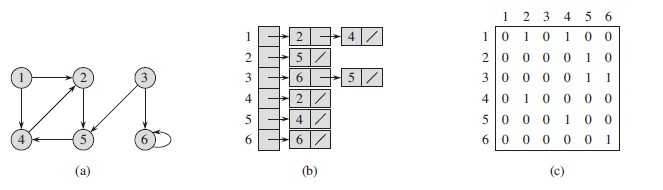
1、邻接矩阵:逻辑结构分为两部分:V和E集合。因此,用一个一维数组存放图中所有顶点数据;用一个二维数组存放顶点间关系(边或弧)的数据,这个二维数组称为邻接矩阵。邻接矩阵又分为有向图邻接矩阵和无向图邻接矩阵。
(1)无向图邻接矩阵:若顶点i到顶点j有一条边,那么aij和aji的值都为1。如上图,一个无向邻接矩阵是一个对称矩阵。
(2)有向图邻接矩阵:若顶点i到顶点j有一条边,那么aij的值为1(若边有权值,这里也可以表示为权值)。
2、邻接链表:邻接链表的思维如下:
(1)图中顶点用一个一维数组存储,当然,顶点也可以用单链表来存储,不过,数组可以较容易的读取顶点的信息,更加方便。
(2)图中每个顶点vi的所有邻接点构成一个线性表,由于邻接点的个数不定,所以,用单链表存储,无向图称为顶点vi的边表,有向图则称为顶点vi作为弧尾的出边表。
3、十字链表
1、深度遍历(DFS)
A、思想:(1)访问未被访问过的顶点A
(2)从A的邻接顶点中选取一个未被访问过的顶点B访问,并将B置为已访问
(3)令A=B,重复(1)(2),直到所有和A相连的顶点遍历完为止
B、伪代码:
(1)递归实现:
visited[A] = true; //初始值为false
B = A的第一个邻接顶点
while(B存在){
if (B未被访问过) 从顶点B出发递归执行该方法
B = A的下一个邻接顶点
}
(2)非递归实现(用一个stack来记录):
stack初始化,visited[]初始化;
对于顶点A,将A入栈,visited[A] = true;
while(stack不为空) {
X = stack.peek(); //取出栈顶元素
if(X存在未被访问过的邻接顶点B){
访问B,visited[B] = true;
B入栈;
} else
stack.poll; //X出栈
}
2、宽度遍历(BFS)
A、思想(用一个Queue保存每层未被访问过的顶点)
(1)顶点V入队列Q
(2)Q为空则遍历结束,否则继续执行下面的
(3)弹出Q的队首元素V,访问V,visited[V] = true;
(4)查找V的第一个邻接顶点A
(5)若A未被访问过,那么将A所有未被访问过的邻接顶点入队
(6)查找V的下一个邻接顶点,转到5;直到V的所有邻接顶点被访问完,转到2.
B、伪代码
初始化队列q,初始化visited[n] = false;
访问顶点V,visited[V] =true; q.add(V); //v入队尾
while(q不为空){
X = q.poll(); //x为队首元素
W = X的第一个邻接顶点
while(W){
if(W未被访问过){
访问W,visited[W] = true;
W入队列;
}
W = X的下一个邻接顶点;’
}
}
标签:访问 不同 第一个 矩阵 部分 str 执行 线性 逻辑
原文地址:http://www.cnblogs.com/271934Liao/p/7262344.html