标签:spec quit tor ring text art minimum plm pos
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 7217 | Accepted: 2965 |
Description
Input
Output
Sample Input
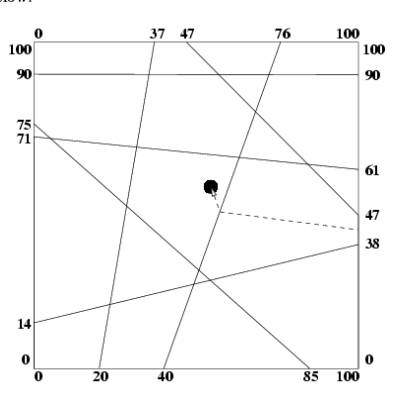
7 20 0 37 100 40 0 76 100 85 0 0 75 100 90 0 90 0 71 100 61 0 14 100 38 100 47 47 100 54.5 55.4
Sample Output
Number of doors = 2
题目大意:
一个正方形的墓葬内有n堵墙,每堵墙的两个顶点都在正方形的边界上,现在这些墙将墓葬分割成了很多小空间,
已知正方形内的一个点上存在宝藏,现在我们要在正方形的外面去得到宝藏,对于每个小空间,我们可以炸开它的任意一条边的中点,
现在给出每堵墙的两个节点的坐标和宝藏的坐标,问如果要得到宝藏,需要炸的墙数最少是多少。
题解:
一道很有意思的计算几何,也比较巧妙。
我们可以发现,其实边界上的出发点,要到达终点,所经过的边数必定是这个点到终点连线与线段的焦点数。因为每一条边都是横穿整个正方形的,所以无论怎么走,都不可能绕过这一条边,毕竟不能走出正方形。
然后就是枚举出发点了,本人一开始将正方形四条边上的点分别排序,然后求中点。这样做很麻烦,仔细一想可以发现,无论是不是从两点的中点开始走,都会到达一个同样的方块。所以枚举中点是没有必要的,直接枚举正方形边上的所有点就可以了。
代码如下:
#include<iostream> #include<cstdio> #include<cstring> #include<cstdlib> #include<cmath> #include<algorithm> using namespace std; int n,ans=2000000000; double xx,yy; struct Vector { double x,y; Vector(){} Vector(double xx,double yy){x=xx;y=yy;} Vector operator+(Vector b) { Vector ans; ans.x=x+b.x;ans.y=y+b.y; return ans; } Vector operator-(Vector b) { Vector ans; ans.x=x-b.x;ans.y=y-b.y; return ans; } double operator*(Vector b) { return x*b.y-b.x*y; } double operator^(Vector b) { return x*b.x+y*b.y; } }; struct node { Vector a,b; }s[31],t; bool check(double x,double y,int i) { t.a=Vector(x,y);t.b=Vector(xx,yy); if(((t.a-t.b)*(s[i].a-t.b))*((t.a-t.b)*(s[i].b-t.b))<0&&((s[i].a-s[i].b)*(t.a-s[i].b))*((s[i].a-s[i].b)*(t.b-s[i].b))<0)return 1; else return 0; } void solve(double x,double y) { int cnt=0; for(int i=1;i<=n;i++) { if(check(x,y,i))cnt++; } ans=min(ans,cnt); } int main() { int i,j; scanf("%d",&n); for(i=1;i<=n;i++)scanf("%lf%lf%lf%lf",&s[i].a.x,&s[i].a.y,&s[i].b.x,&s[i].b.y); scanf("%lf%lf",&xx,&yy); for(i=0;i<=100;i++) { solve(i,100); solve(i,0); solve(0,i); solve(100,i); } printf("Number of doors = %d\n",++ans); return 0; }
标签:spec quit tor ring text art minimum plm pos
原文地址:http://www.cnblogs.com/huangdalaofighting/p/7270310.html