标签:style blog http color os io 使用 strong ar
摘要:本文讨论了最长公共子串的的相关算法的时间复杂度,然后在后缀数组的基础上提出了一个时间复杂度为o(n^2*logn),空间复杂度为o(n)的算法。该算法虽然不及动态规划和后缀树算法的复杂度低,但其重要的优势在于可以编码简单,代码易于理解,适合快速实现。
首先,来说明一下,LCS通常指的是公共最长子序列(Longest Common Subsequence,名称来源参见《算法导论》原书第3版p223),而不是公共最长子串(也称为最长公共子串)。
最长公共子串问题是在文本串、模式串中寻找共有的一个最长的子串,如文本串text=“abcbcedf”,pattern=“ebcbcdf”,则最长公共子串为“bcbc”,长度为4。
最长公共子串的解法很多,有蛮力搜索法、动态规划法、后缀数组法、后缀树法。本文着重提后缀数组法,其他方法可以自行百度。
蛮力搜索法
1 int enum_longestCommonSubstring(char *text,char *pattern) 2 { 3 if(!text || !pattern) return 0; //nullptr 4 int tlen=strlen(text),plen=strlen(pattern); 5 if(0==tlen || 0==plen) return 0; //empty string 6 int maxLEN=0,i=0,j=0,ofs=0; 7 for(i=0;i<tlen && (tlen-i>=maxLEN);++i) 8 for(j=0;j<plen && (plen-j>=maxLEN); ++j) 9 if( *(text+i)==*(pattern+j) ) 10 { 11 ofs=1; 12 while((i+ofs)<tlen&&(j+ofs)<plen&&*(text+ofs)==*(pattern+ofs)) 13 { ++ofs; } 14 if(ofs>maxLEN) maxLEN=ofs; //update 15 } 16 return maxLEN; 17 }
记文本串长度为m,模式串长度为n,则暴力搜索法时间复杂度为o(m*n*Min(m,n)),空间复杂度o(1)。在子串匹配问题上,如果使用KMP算法,则算法效率可以提高。
动态规划
动态规划求解最长公共子串问题的时间复杂度为o(m*n),经过优化后的动态规划算法可以达到o(Min(m,n))的空间复杂度
参见http://www.cnblogs.com/ider/p/longest-common-substring-problem-optimization.html
后缀数组
利用排序后的后缀数组(suffix array)来求解最长公共子串步骤为:
一,拼接文本串和模式串得到一个新的串X;
二,将X的所有后缀数组存入sa;(文本串长度为m,模式串长n。步骤二时间复杂度o(m+n)
三,对sa进行排序;
四,计算sa中相邻的子串的最长公共前缀长度(时间复杂度o((m+n)*Min(m,n)))
注:为了避免得到单个串的最长重复子串,在步骤四种参与比较的两个子串应该为一个是文本串的子串,另一个为模式串的子串。因此,在步骤一、二中就应该附加记录位来处理。
《后缀数组——————处理字符串的有力工具处理字符串的有力工具》罗穗骞介绍了使用基数排序来排序后缀数组的方法,排序时间复杂度(m+n)*log(m+n)。因此,使用使用后缀数组+基数排序得到的算法的时间复杂度为o((m+n)*Min(m,n))(步骤四决定最大时间复杂度)。但是,该方法较复杂,不容易掌握,在此处,我提出一种后缀数组+C标准库sort排序的算法,其排序时间复杂度为o(Min(m,n)*(m+n)*log(m+n)),因此,算法整体的时间复杂度为o(Min(m,n)*(m+n)*log(m+n))(由步骤三决定最大时间复杂度),此外,该算法空间复杂度为o(m+n)。 “后缀数组+快排”算法时间复杂低于“后缀数组+基数排序”的时间复杂度,但优点在于利用标准库sort+strcmp来实现排序,代码简单,算法更容易理解。代码如下:
1 #include<stdio.h> 2 #include<iostream> 3 #include<string.h> 4 #include<algorithm> 5 using namesapce std; 6 int suffixArrayQsort_longestCommonSubstring(char *text,char *pattern) 7 { 8 if(!text || !pattern) return 0; //nullptr 9 int tlen=strlen(text),plen=strlen(pattern),i,j; 10 if(0==tlen || 0==plen) return 0; //empty string 11 12 enum ATTRIB{TEXT,PATTERN}; 13 struct absInfo 14 { 15 char *head; 16 ATTRIB attr; //tag 17 int len; 18 absInfo():head(NULL),attr(TEXT),len(0){} 19 absInfo(char *phead,ATTRIB attrib,int length):head(phead),attr(attrib),len(length){} 20 bool operator < (const absInfo &b) 21 { 22 return strcmp(head,b.head)<0; 23 } 24 static void display(const absInfo &a) 25 { 26 printf("size:%d type:%-7s ",a.len, (a.attr==TEXT?"TEXT":"PATTERN") ); 27 printf("%s\n",a.head); 28 } 29 }*sa; 30 31 //step 2:build the suffix array 32 sa=new absInfo[tlen+plen]; 33 for(i=0;i<tlen;++i) 34 { 35 sa[i].head=text+i; 36 sa[i].attr=TEXT; 37 sa[i].len=tlen-i; 38 } 39 for(j=0;j<plen;++j) 40 { 41 sa[j+tlen].head=pattern+j; 42 sa[j+tlen].attr=PATTERN; 43 sa[j+tlen].len=plen-j; 44 } 45 46 //step 3:use sort() to sort the sa 47 puts("before sort, the sa is:"); for_each(sa,sa+tlen+plen,absInfo::display); 48 sort(sa,sa+tlen+plen); 49 puts("after sort, the sa is:"); for_each(sa,sa+tlen+plen,absInfo::display); 50 51 //step 4:compare 52 int maxLEN=0,rec=0; 53 for(i=0;i<tlen+plen-1;i++) 54 { 55 if(sa[i].attr==sa[i+1].attr) continue; 56 if(sa[i].len<=maxLEN || sa[i+1].len<=maxLEN) continue; 57 rec=0; 58 while(rec<sa[i].len && rec<sa[i+1].len && *(sa[i].head+rec)==*(sa[i+1].head+rec) ) 59 ++rec; 60 if(rec>maxLEN) maxLEN=rec; //update 61 } 62 //release memory resource and return 63 delete [] sa; sa=NULL; 64 return maxLEN; 65 }
注:1,absInfo结构中len字段不是必须的,设置此字段只是为了在代码56行处做一个搜索剪枝操作。
2,稍微改动代码就能在算法中给出公共子串的值(对示例来说就是给出“bcbc"),通过absInfo的len字段和maxLEN值也可以在o(1)的时间复杂度内计算出公共子串分别在文本串和模式串中的位置
运行结果:
当文本串text=“abcbcedf”,pattern=“ebcbcdf”时,代码运行如下图所示:
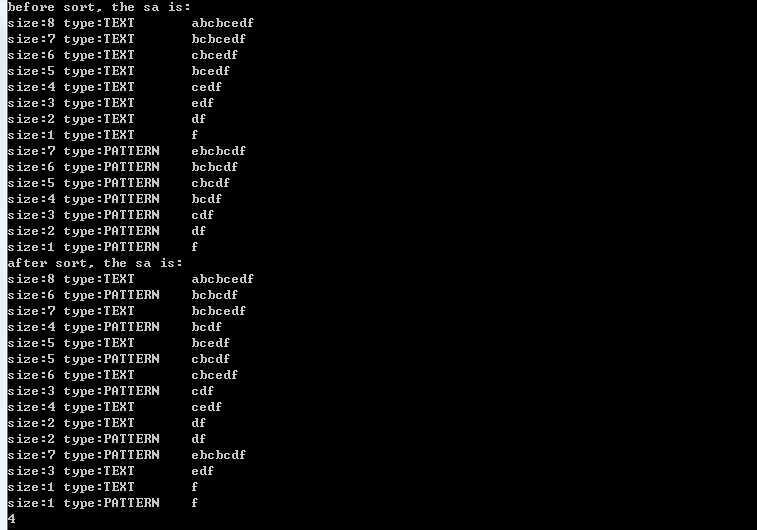
从代码可以看出,“后缀数组+qsort排序”实现最长公共子串具有编码简单的特点,空间复杂度为o(m+n)
后缀树
后缀树以及广义的后缀树算法读者可以自行搜索。
利用后缀数组(suffix array)求最长公共子串(longest common substring)
标签:style blog http color os io 使用 strong ar
原文地址:http://www.cnblogs.com/youngzii/p/algorithm.html