标签:说明 int http sum 约数 for -- const ima
for i=1 to n
for j=1 to n
sum+=gcd(i,j)给出n求sum. gcd(x,y)表示x,y的最大公约数.
输入格式:
n
输出格式:
sum
2
5
数据范围
30% n<=3000
60% 7000<=n<=7100
100% n<=100000
题目的意思大概是这样的
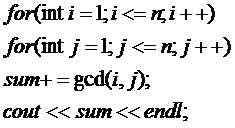
O(n2)枚举当然是不行的啦。
考虑枚举k,求gcd为k的“数对”的个数。
而可以证明gcd为k的“数对”的个数为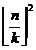
利用容斥把gcd为2k,3k,4k的“数对”的个数减去就好啦?
注意k要从大到小枚举。
1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 using namespace std; 5 6 typedef long long ll; 7 8 const int maxn=100005; 9 10 int n; 11 ll dp[maxn],ans=0; 12 13 int main(){ 14 scanf("%d",&n); 15 for(int i=n;i>0;i--){ 16 dp[i]=1ll*(n/i)*(n/i); 17 for(int j=(i<<1);j<=n;j+=i) 18 dp[i]-=dp[j]; 19 ans+=dp[i]*i; 20 } 21 printf("%lld\n",ans); 22 return 0; 23 }
标签:说明 int http sum 约数 for -- const ima
原文地址:http://www.cnblogs.com/ZYBGMZL/p/7271899.html