标签:return 是什么 函数 scanf image span nbsp 节点 bool
题目真的草率,额,没办法。
第一题是meet in middle,一直以为时间会炸,结果可以裸跑80,正解就是优化的暴力,服了,自己还特判了大于45,就学了辉哥的宽搜堆,就是以到m的距离为估价函数。
炸了,炸了50分
1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 long long w,ans,maxs,a[105]; 5 int cnt,n,m1,m2,num1,num2,cnt1,cnt2,top,q1[60000005],q2[60000005]; 6 void dfs1(int t,long long sum) 7 { 8 if (sum>w) return; 9 if (t>m1) 10 { 11 q1[++cnt1]=sum; 12 return; 13 } 14 dfs1(t+1,sum+a[t]); 15 dfs1(t+1,sum); 16 } 17 void dfs2(int t,long long sum) 18 { 19 if (sum>w) return; 20 if (t>m2) 21 { 22 q2[++cnt2]=sum; 23 return; 24 } 25 dfs2(t+1,sum+a[t+m1]); 26 dfs2(t+1,sum); 27 } 28 int main() 29 { 30 freopen("brick.in","r",stdin); 31 freopen("brick.out","w",stdout); 32 scanf("%lld%d",&w,&cnt); 33 for (int i=1; i<=cnt; i++) 34 { 35 long long x; 36 scanf("%lld",&x); 37 if (x<=w) 38 { 39 maxs+=x; 40 a[++n]=x; 41 } 42 } 43 if (maxs<=w) 44 { 45 printf("%lld\n",maxs); 46 fclose(stdin); fclose(stdout); 47 return 0; 48 } 49 m1=n/2; 50 m2=n-m1; 51 dfs1(1,0); 52 dfs2(1,0); 53 sort(q1+1,q1+cnt1+1); 54 sort(q2+1,q2+cnt2+1); 55 q1[1]=q1[1]; 56 num1=1; 57 for (int i=2; i<=cnt1; i++) 58 if (q1[i]!=q1[num1]) q1[++num1]=q1[i]; 59 q2[1]=q2[1]; 60 num2=1; 61 for (int i=2; i<=cnt2; i++) 62 if (q2[i]!=q2[num2]) q2[++num2]=q2[i]; 63 top=num2; 64 ans=max(q1[num1],q2[num2]); 65 for (int i=1; i<=num1; i++) 66 { 67 long long s=q1[i]; 68 while (q2[top]+s>w) top--; 69 if (top==0) break; 70 if (q1[i]+q2[top]>ans) ans=q1[i]+q2[top]; 71 } 72 printf("%lld\n",ans); 73 fclose(stdin); fclose(stdout); 74 return 0; 75 }
第二题正解是贪心,就是刚开始是先全横着走,然后最后向上走,那么贪心思想是什么呢?就是当前这里向上走几格,就是斜着走几个,发现越斜着走,相差花费越大,
所以就有了贪心思想,然后用堆优化,每次取相差最小的,如果增加的费用比1/u还大的话就直接退出就可以了,因为当前最小比不上直走,所有根据单调,以后的不可能
会更小,然后就好了。
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<queue> 5 #include<cmath> 6 #include<iostream> 7 using namespace std; 8 9 const int NN=50007,MM=100007; 10 11 int n,Y; 12 int wi[NN],a[NN]; 13 double u,vi[NN]; 14 15 struct Node 16 { 17 double fee; 18 int tall,num; 19 }; 20 struct cmp 21 { 22 bool operator()(Node x,Node y) 23 { 24 return x.fee>y.fee; 25 } 26 }; 27 priority_queue<Node,vector<Node>,cmp >q; 28 29 double oula(int x,int y) 30 { 31 return sqrt(x*x+y*y); 32 } 33 int main() 34 { 35 freopen("river.in","r",stdin); 36 freopen("river.out","w",stdout); 37 38 scanf("%d%d%lf",&n,&Y,&u); 39 for (int i=1;i<=n;i++) scanf("%d",&wi[i]); 40 for (int i=1;i<=n;i++) scanf("%lf",&vi[i]); 41 42 double ans=0; 43 for (int i=1;i<=n;i++) ans+=wi[i]*1.0/vi[i]; 44 45 ans+=Y*1.0/u; 46 47 for (int i=1;i<=n;i++) 48 { 49 Node x; 50 x.tall=1,x.fee=oula(wi[i],1)/vi[i]-oula(wi[i],0)/vi[i],x.num=i; 51 q.push(x); 52 } 53 for (int i=1;i<=Y;i++) 54 { 55 Node x=q.top(); 56 q.pop(); 57 if (x.fee>(1.0/u)) break; 58 ans=ans-1.0/u+x.fee; 59 x.tall++,x.fee=(double)(oula(wi[x.num],x.tall)-oula(wi[x.num],x.tall-1))/vi[x.num]; 60 q.push(x); 61 } 62 printf("%.4f",ans); 63 }
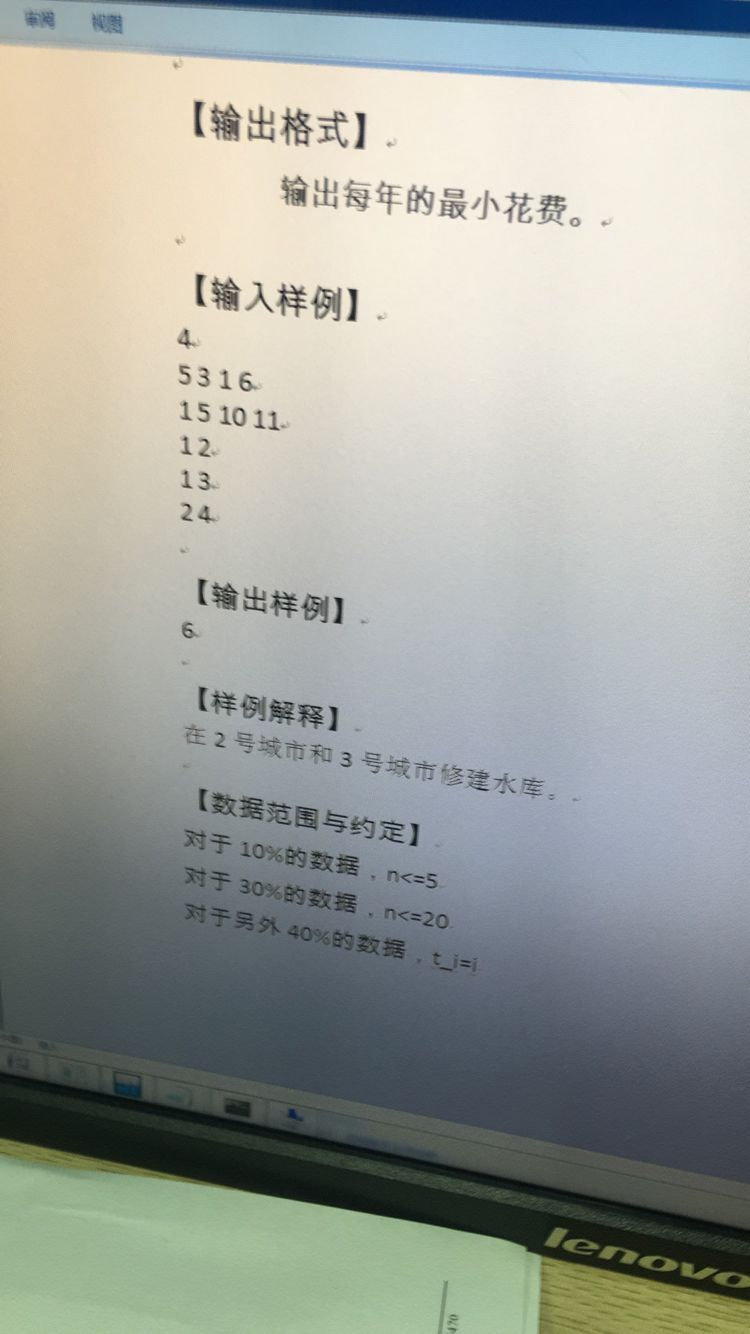
最后一道题就是树形dp,以前还做到过,是灰色的记忆,那套题目里面的,f[i][j]表示i号节点由j来运水的最优解,然后best[i]表示以i为根的子树的最优解,然后每次做完f[u][i]枚举通水点,
这样就更新一下best[i],转移就是f[u][i]=min(f[v][i]-c[i],best[v]),表示当前点以i为通水点的最小值只可能从v的最优解或者v也是以i为通水点,然后减去c[i]费用,这两个只里面产生。
然后dp就可以了,n次bfs预处理出各点对之间距离。
1 #include<cstdio> 2 #include<algorithm> 3 #include<cmath> 4 #include<iostream> 5 #include<cstring> 6 #include<queue> 7 using namespace std; 8 9 typedef pair<int,int>fzy; 10 const int INF=1e9+7,NN=1007; 11 12 int n; 13 int c[NN],t[NN],best[NN],dp[NN][NN],dis[NN][NN]; 14 int cnt=0,head[NN],next[NN*2],rea[NN*2],vis[NN]; 15 void bfs(int S) 16 { 17 memset(vis,0,sizeof(vis)); 18 queue<fzy>q; 19 q.push(make_pair(S,0)); 20 vis[S]=1; 21 while(!q.empty()) 22 { 23 fzy u=q.front(); 24 q.pop(); 25 dis[S][u.first]=u.second; 26 for (int i=head[u.first];i!=-1;i=next[i]) 27 { 28 int v=rea[i]; 29 if (vis[v]==0) 30 { 31 vis[v]=1; 32 q.push(make_pair(v,u.second+1)); 33 } 34 } 35 } 36 } 37 void dfs(int u,int fa) 38 { 39 for (int i=head[u];i!=-1;i=next[i]) 40 { 41 int v=rea[i]; 42 if (v==fa) continue; 43 dfs(v,u); 44 } 45 for (int i=1;i<=n;i++) 46 { 47 for (int j=head[u];j!=-1;j=next[j]) 48 { 49 int v=rea[j]; 50 if (fa==v) continue; 51 dp[u][i]+=min(dp[v][i]-c[i],best[v]); 52 } 53 dp[u][i]=dp[u][i]+c[i]+t[dis[u][i]]; 54 best[u]=min(dp[u][i],best[u]); 55 } 56 } 57 void add(int u,int v) 58 { 59 next[++cnt]=head[u]; 60 head[u]=cnt; 61 rea[cnt]=v; 62 } 63 int main() 64 { 65 freopen("reservoir.in","r",stdin); 66 freopen("reservoir.out","w",stdout); 67 68 cnt=0; 69 memset(head,-1,sizeof(head)); 70 scanf("%d",&n); 71 for (int i=1;i<=n;i++) 72 scanf("%d",&c[i]); 73 for (int i=1;i<=n;i++) 74 scanf("%d",&t[i]); 75 int x,y; 76 for(int i=1;i<n;i++) 77 { 78 scanf("%d%d",&x,&y); 79 add(x,y),add(y,x); 80 } 81 for (int i=1;i<=n;i++) bfs(i); 82 for (int i=1;i<=n;i++) best[i]=INF; 83 dfs(1,-1); 84 printf("%d\n",best[1]); 85 }
标签:return 是什么 函数 scanf image span nbsp 节点 bool
原文地址:http://www.cnblogs.com/fengzhiyuan/p/7287309.html