标签:long sig list style 判断 分享 没有 ret 旋转
伸展树
1、在伸展树上的一般操作都基于伸展操作:假设想要对一个二叉查找树执行一系列的查找操作,为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。因此,在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。伸展树应运而生。伸展树是一种自调整形式的二叉查找树,它会沿着从某个节点到树根之间的路径,通过一系列的旋转把这个节点搬移到树根去。
2、操作
(1)伸展操作
伸展操作Splay(x,S)是在保持伸展树有序性的前提下,通过一系列旋转将伸展树S中的元素x调整至树的根部。在调整的过程中,要分以下三种情况分别处理:
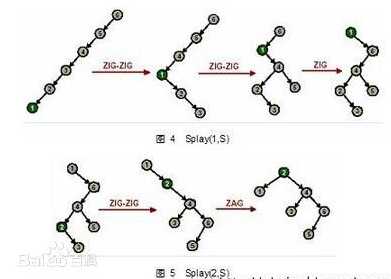
(2)查找操作
Find(x,S):判断元素x是否在伸展树S表示的有序集中。
操作:在伸展树中查找元素x。如果x在树中,则再执行Splay(x,S)调整伸展树。
(3)插入操作
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<cmath>
#include<iostream>
#include<sstream>
#include<iterator>
#include<algorithm>
#include<string>
#include<vector>
#include<set>
#include<map>
#include<stack>
#include<deque>
#include<queue>
#include<list>
#define lowbit(x) (x & (-x))
const double eps = 1e-8;
inline int dcmp(double a, double b){
if(fabs(a - b) < eps) return 0;
return a > b ? 1 : -1;
}
typedef long long LL;
typedef unsigned long long ULL;
const int INT_INF = 0x3f3f3f3f;
const int INT_M_INF = 0x7f7f7f7f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const LL LL_M_INF = 0x7f7f7f7f7f7f7f7f;
const int dr[] = {0, 0, -1, 1, -1, -1, 1, 1};
const int dc[] = {-1, 1, 0, 0, -1, 1, -1, 1};
const int MOD = 1e9 + 7;
const double pi = acos(-1.0);
const int MAXN = 32767 + 10;
const int MAXT = 10000 + 10;
using namespace std;
int root;//根结点标号,初始时是值为0的虚设根结点
int cnt;
int child[MAXN << 2][2];//左右子结点标号,按输入顺序从1开始依次标号
int value[MAXN << 2];//结点值
int pre[MAXN << 2];//父结点标号
void newNode(int &node, int fa, int x){
node = ++cnt;
pre[node] = fa;
value[node] = x;
child[node][0] = child[node][1] = 0;
}
void Rorate(int x, int dir){//dir:1--右旋,0--左旋
int y = pre[x];//y是x的父结点,该函数内以下注释以右旋为例
child[y][!dir] = child[x][dir];//将x的右子结点作为y的左子结点
pre[child[x][dir]] = y;//让x的右结点认y做父结点
if(pre[y]){//若y的父结点不是虚设根结点,则让y的父结点认x做子结点,左右取决于y原先是其父结点的左右子结点
child[pre[y]][child[pre[y]][1] == y] = x;
}//若y的父结点是虚设根结点,则y无所谓左右子结点,此时只需要立x为真正的根结点即可,真正根结点的一大标志是父结点标号为0
pre[x] = pre[y];//让x认y的父结点为父结点
child[x][dir] = y;//将y作为x的右子结点
pre[y] = x;//让y认x为父结点
}
void splay(int x, int goal){
while(pre[x] != goal){
int y = pre[x];
if(pre[y] == goal){//单旋
Rorate(x, child[y][0] == x);
}
else{
int dir = (child[pre[y]][0] == y);//y的旋转方向
if(child[y][dir] == x){//之字形旋转
Rorate(x, !dir);
Rorate(x, dir);
}
else{//一字形旋转
Rorate(y, dir);
Rorate(x, dir);
}
}
}
if(goal == 0) root = x;//更新根结点标号
}
int getPre(int x){//求前驱结点值
int tmp = child[x][0];
if(tmp == 0) return -1;//前驱结点为虚设根结点或不存在
while(child[tmp][1]) tmp = child[tmp][1];
return value[tmp];
}
int getSuc(int x){//求后继结点值
int tmp = child[x][1];
if(tmp == 0) return -1;////后继结点为虚设根结点或不存在
while(child[tmp][0]) tmp = child[tmp][0];
return value[tmp];
}
bool Insert(int x){
if(!root){
newNode(root, 0, x);
}
else{
int tmp = root;
if(value[tmp] == x){//树中已存在该结点值,不必再插入
splay(tmp, 0);
return false;
}
while(child[tmp][x > value[tmp]]){//child[tmp][0]--左,child[tmp][0]--右
tmp = child[tmp][x > value[tmp]];
if(value[tmp] == x){//树中已存在该结点值,不必再插入
splay(tmp, 0);
return false;
}
}
newNode(child[tmp][x > value[tmp]], tmp, x);
splay(child[tmp][x > value[tmp]], 0);
}
return true;
}
int main(){
int n;
scanf("%d", &n);
int x, ans = 0;
for(int i = 0; i < n; ++i){
scanf("%d", &x);
if(!i){
Insert(x);
ans += x;
}
else{
if(Insert(x)){
int prenode = getPre(root);
int sucnode = getSuc(root);
int tmp = INT_INF;
if(prenode != -1) tmp = min(tmp, x - prenode);
if(sucnode != -1) tmp = min(tmp, sucnode - x);
ans += tmp;
}
}
}
printf("%d\n", ans);
return 0;
}
后续待更新~
标签:long sig list style 判断 分享 没有 ret 旋转
原文地址:http://www.cnblogs.com/tyty-Somnuspoppy/p/7285498.html