Codeforces 235B. Let's Play Osu!

You‘re playing a game called Osu! Here‘s a simplified version of it. There are n clicks in a game. For each click there are two outcomes: correct or bad. Let us denote correct as "O", bad as "X", then the whole play can be encoded as a sequence of n characters "O" and "X".

Using the play sequence you can calculate the score for the play as follows: for every maximal consecutive "O"s block, add the square of its length (the number of characters "O") to the score. For example, if your play can be encoded as "OOXOOOXXOO", then there‘s three maximal consecutive "O"s block "OO", "OOO", "OO", so your score will be 22?+?32?+?22?=?17. If there are no correct clicks in a play then the score for the play equals to 0.

You know that the probability to click the i-th (1?≤?i?≤?n) click correctly is pi. In other words, the i-th character in the play sequence has piprobability to be "O", 1?-?pi to be "X". You task is to calculate the expected score for your play.

Input

The first line contains an integer n (1?≤?n?≤?105) — the number of clicks. The second line contains n space-separated real numbersp1,?p2,?...,?pn (0?≤?pi?≤?1).

There will be at most six digits after the decimal point in the given pi.

Output

Print a single real number — the expected score for your play. Your answer will be considered correct if its absolute or relative error does not exceed 10?-?6.

Sample test(s)

input
3
0.5 0.5 0.5

output
2.750000000000000

input
4
0.7 0.2 0.1 0.9

output
2.489200000000000

input
5
1 1 1 1 1

output
25.000000000000000

Note

For the first example. There are 8 possible outcomes. Each has a probability of 0.125.

"OOO" ?→? 32?=?9;
"OOX" ?→? 22?=?4;
"OXO" ?→? 12?+?12?=?2;
"OXX" ?→? 12?=?1;
"XOO" ?→? 22?=?4;
"XOX" ?→? 12?=?1;
"XXO" ?→? 12?=?1;
"XXX" ?→? 0.

So the expected score is 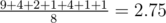$bubuko.com,布布扣$

/** * Created by ckboss on 14-9-3. */ import java.util.*; public class N { public static void main(String[] args){ Scanner in=new Scanner(System.in); int n=in.nextInt(); double ans=0,pre=0,now=0; for(int i=1;i<=n;i++) { now=in.nextDouble(); pre=pre*now; ans+=2*pre+now; pre=pre+now; } System.out.println(ans); } }

Codeforces 235B. Let's Play Osu!

235B - Let‘s Play Osu!