标签:mit word 根据 ted stat min 状态 write null
Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2.
(each operation is counted as 1 step.) You have the following 3 operations permitted on a word: a) Insert a character b) Delete a character c) Replace a character
Given word1 ="mart"and word2 ="karma", return3.
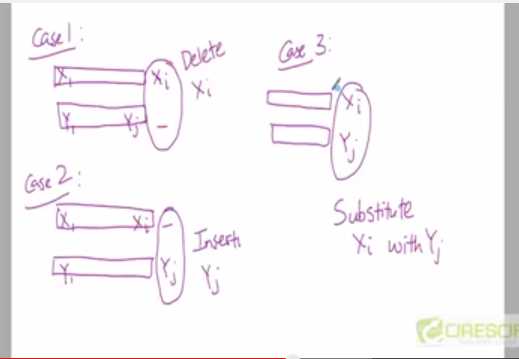
res[i][j]表示Edit Distance between X数组的前i个元素以及Y数组的前j个元素,或者the minimum # of operations to convert X前i个元素 into Y的前j个元素
因为对于Xi 和 Yj,操作无非是 insert, delete, replace三种,所以递归式就是三项:根据上面这个图很清楚:res[i][j] = min{res[i-1][j]+1, res[i][j-1]+1, Xi == Yj ? res[i-1][j-1] : res[i-1][j-1] + 1}
public int minDistance(String word1, String word2) {
// write your code here
// state
int m = word1.length(), n = word2.length();
/*if (word1 == null || word2 == null || )*/
int[][] f = new int[m + 1][n + 1];
// initialize
f[0][0] = 0;
for (int i = 1; i <= m; i++) {
f[i][0] = i;
}
for (int i = 1; i <= n; i++) {
f[0][i] = i;
}
// function
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
f[i][j] = /*f[i - 1][j - 1]*/ Math.min(f[i - 1][j - 1], Math.min(f[i - 1][j] + 1, f[i][j - 1] + 1));
} else {
f[i][j] = Math.min(f[i - 1][j - 1] + 1, Math.min(f[i - 1][j] + 1, f[i][j - 1] + 1));
}
}
}
return f[m][n];
}
写好状态后, 想想与上一个状态怎么用题意联系起来, 上一个状态常常是遍历的上一个状态, 字符串问题常常要考虑上一个字母是否匹配来分情况讨论
标签:mit word 根据 ted stat min 状态 write null
原文地址:http://www.cnblogs.com/apanda009/p/7291363.html