标签:规律 net 也会 问题 https near sam 参考 说明
一、协方差
可以通俗的理解为:两个变量在变化过程中是同方向变化?还是反方向变化?同向或反向程度如何?(你变大,同时我也变大,说明两个变量是同向变化的)
协方差定义:Cov(X,Y)=E[(X-E(X))(Y-E(Y))]
公式简单翻译一下是:如果有X,Y两个变量,每个时刻的“X值与其均值之差”乘以“Y值与其均值之差”得到一个乘积,再对这每时刻的乘积求和并求出均值(这里求“期望”简单认为就是求均值了)。
如果X、Y变化方向相同,即当X大于其均值时,Y也大于其均值,当X小于其均值时,Y也小于其均值,在这两种情况下,乘积为正。如果X、Y的变化方向一直保持相同,X变大的时候,Y也变大,X变小的时候,Y也变小,则协方差为正;
如果X、Y变化方向一直相反,则协方差为负;
如果X、Y变化方向之间相互无规律,则可能某一时刻(X-E(X))(Y-E(Y))为正,而另一时刻的(X-E(X))(Y-E(Y))为负,累计以后正负项抵消,最后求出的平均值就是协方差,通过协方差的大小,就可以判断两个变量变化同向或者反向的程度了。
总结一下,如果协方差为正,说明X,Y同向变化,协方差越大说明同向程度越高;如果协方差为负,说明X,Y反向运动,协方差越小说明反向程度越高。
二、相关系数
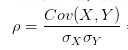
公式翻译一下:相关系数就是用X、Y的协方差除以X的标准差和Y的标准差。(标准差是方差的算术平方根)
所以,相关系数也可以看成协方差:一种剔除了两个变量量纲影响、标准化后的特殊协方差。
既然是一种特殊的协方差,那它:
1、也可以反映两个变量变化时是同向还是反向,如果同向变化就为正,反向变化就为负。
2、由于它是标准化后的协方差,因此更重要的特性来了:它消除了两个变量变化幅度的影响,而只是单纯反应两个变量每单位变化时的相似程度。
总结一下,对于两个变量X、Y,当他们的相关系数为1时,说明两个变量变化时的正向相似度最大,即,你变大一倍,我也变大一倍;你变小一倍,我也变小一倍。也即是完全正相关(以X、Y为横纵坐标轴,可以画出一条斜率为正数的直线,所以X、Y是线性关系的)。随着他们相关系数减小,两个变量变化时的相似度也变小,当相关系数为0时,两个变量的变化过程没有任何相似度,也即两个变量无关。当相关系数继续变小,小于0时,两个变量开始出现反向的相似度,随着相关系数继续变小,反向相似度会逐渐变大。当相关系数为-1时,说明两个变量变化的反向相似度最大,即,你变大一倍,我变小一倍;你变小一倍,我变大一倍。也即是完全负相关(以X、Y为横纵坐标轴,可以画出一条斜率为负数的直线,所以X、Y也是线性关系的)。
参考链接:http://www.mathsisfun.com/data/correlation.html
一般我们讲的相关系数,其实叫皮尔逊相关系数(Pearson correlation coefficient),wiki关于这个系数的解释是:
The correlation coefficient ranges from ?1 to 1. A value of 1 implies that a linear equation describes the relationship between X and Y perfectly, with all data points lying on a line for which Y increases as X increases. A value of ?1 implies that all data points lie on a line for which Y decreases as X increases. A value of 0 implies that there is no linear correlation between the variables.

如图(右上)所示,非线性相关也会导致线性相关系数很大;
好吧,你退一步,转而问:如果两个变量的相关系数很大(0.816),那能不能说两者相关呢? 答案还是不能,为什么? 因为如图(右下)所示,很可能是一个离群点(outlier)导致了相关系数变得很大。
这也不能那也不能,那怎么办?(你一定要画出图来看才行,后面会深入解释)

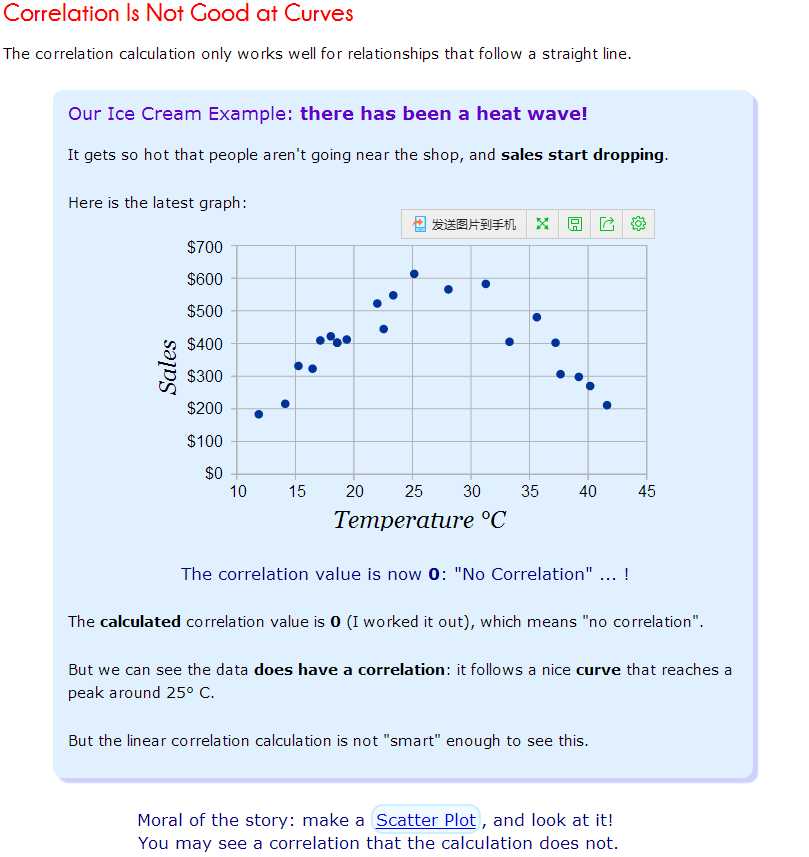
上图的相关系数计算结果为0,但你能说冰激凌的销量和温度不相关吗?
所以, pearson correlation coefficient = 0只能说不是线性相关,但说不定会有更复杂的相关关系(非线性相关)
总结:如果两个变量本身就是线性的关系,那么皮尔逊相关系数ok没问题,绝对值大的就是相关性强,小的就是相关性弱;
但在你不知道这两个变量是什么关系的情况下,即使算出皮尔逊相关系数,发现很大,也不能说明那两个变量线性相关,甚至不能说他们相关,你一定要画出图来看才行,这就是为什么我们说眼见为实和数据可视化的重要性。
参考链接:
http://blog.csdn.net/witforeveryang/article/details/42585791
https://en.wikipedia.org/wiki/Pearson_correlation_coefficient
理解:在不存在离群点的情况下,相关系数反应的是两个变量之间的线性相关程度,线性相关程度高低与变量之间有没有其他非线性相关性无关。
标签:规律 net 也会 问题 https near sam 参考 说明
原文地址:http://www.cnblogs.com/guo-xiang/p/7295301.html