标签:可见 一个 最小值 函数 cat 关键点 output 去重 如何
转载请注明:
题目大意:
题目传送门:UVa 221 Urban Elevations
给出城市中建筑物的x, y 坐标的最小值:x,y , 再给出其以左下角为坐标原点的关于x轴、y轴上的长度 w, 和 d,最后给出建筑物的高度 h,将建筑物的正视图中,能够看到的建筑物的id打印出来:要求先打印x小的,当x相同时,打印y小的。为了简化,假定建筑物都是长方体。同时,每个输出之间要用一个空行隔开 One blank line must separate output from consecutive input records.(一开始没注意审题,wa在这了┭┮﹏┭┮)
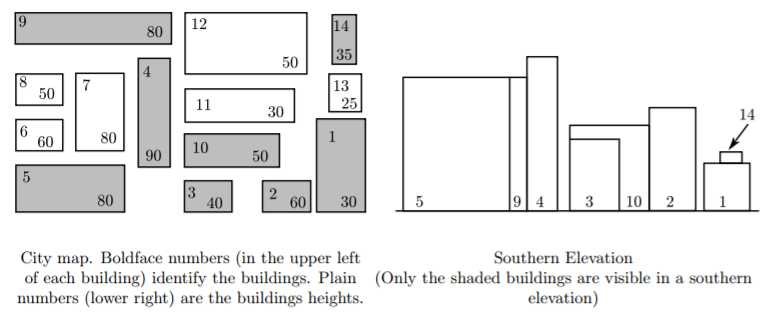
思路:
首先,这个题我本来没什么思路,还是不得不参考一波刘汝佳老师的思路
本题最大的收获是初步认识了 “离散化” :将无限转化为有限的方法。
代码如下:
1 // UVa 221 Urban Elevations 2 // Ruiyuan Lu 3 #include<cstdio> 4 #include<algorithm> 5 using namespace std; 6 7 const int maxn = 100 + 5; 8 double x[maxn*2]; // each building has 2 coordinates of x axis 9 int n; // number of the buildings 10 11 struct Building{ 12 int id; 13 double x, y, w, d, h; // w: means x_len, d:depth means y_len, h:height 14 bool operator < (const Building& b) const { // sort for output 15 return x < b.x || (x == b.x && y < b.y); 16 } 17 }b[maxn]; 18 19 bool cover(int i, double mx); // determine if the mx is in the range of building‘s x coordinate 20 bool visible(int i, double mx); // i: the index of buildings; mx: middle x coordinate of an interval 21 22 int main(){ 23 int cnt = 0; 24 while(scanf("%d", &n) == 1 && n > 0){ 25 for(int i=0; i<n;i++){ 26 scanf("%lf%lf%lf%lf%lf", &b[i].x, &b[i].y, &b[i].w, &b[i].d, &b[i].h); 27 b[i].id = i + 1; 28 x[i*2] = b[i].x; x[i*2+1] = b[i].x + b[i].w; // init x for discretization 29 } 30 sort(x, x+n*2); // sort before unique() is invoked 31 sort(b, b+n); // sort for output 32 int m = unique(x, x+maxn*2) - x; // get the number of unique x in the array 33 // print result 34 if(cnt++)printf("\n"); // print the ‘\n‘ for last output 35 printf("For map #%d, the visible buildings are numbered as follows:\n%d", cnt, b[0].id); 36 for(int i=1;i<n;i++) 37 for(int j=1;j<m;j++) // check each building if it is visible in any interval of m intervals 38 if(visible(i, (x[j-1] + x[j]) / 2)){ 39 printf(" %d", b[i].id); 40 break; 41 } 42 printf("\n"); // as they required: One blank line must separate output from consecutive input records. 43 } 44 } 45 46 bool cover(int i, double mx){ 47 return b[i].x <= mx && b[i].x + b[i].w >= mx; 48 } 49 50 bool visible(int i, double mx){ 51 if(!cover(i, mx)) return false; 52 for(int j=0;j<n;j++) 53 if(b[j].y < b[i].y && b[j].h >= b[i].h && cover(j, mx)) return false; 54 return true; 55 }

啦啦啦,今天就到这里啦~改天见*★,°*:.☆( ̄▽ ̄)/$:*.°★* 。
UVa 221 Urban Elevations 城市正视图 离散化初步 无限化有限
标签:可见 一个 最小值 函数 cat 关键点 output 去重 如何
原文地址:http://www.cnblogs.com/luruiyuan/p/7296661.html