现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
输入格式:
输入数据包括城镇数目正整数NN(\le 1000≤1000)和候选道路数目MM(\le 3N≤3N);随后的MM行对应MM条道路,每行给出3个正整数,分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见,城镇从1到NN编号。
输出格式:
输出村村通需要的最低成本。如果输入数据不足以保证畅通,则输出-1?1,表示需要建设更多公路。
输入样例:
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
输出样例:
12
----------分析-----------------------------
这是一个典型的最小生成树的问题。当时去厦大夏令营面试的时候遇到这个问题,我束手无策。今天下午花了一个下午+晚上的时候才算搞清楚了些Prime算法。
算法的思路可自行百度。这里贴出我写的代码
1 #include <stdio.h> 2 #define MAX_VEX_NUM 101 3 #define MAX_VALUE 9999 4 5 typedef struct Graph 6 { 7 int vex[MAX_VEX_NUM][MAX_VEX_NUM]; 8 int vexNum; 9 int arsNum; 10 }Graph; 11 12 13 struct closedeg 14 { 15 int vex; 16 int lowcost; 17 } closedeg[MAX_VEX_NUM]; 18 19 void init(Graph *G) 20 { 21 int i, j; 22 for(i = 1; i <= G->vexNum; i++) 23 for(j = 1; j <= G->vexNum; j++) 24 G->vex[i][j] = MAX_VALUE; 25 } 26 27 int isLianTong(Graph *G) 28 { 29 int i, j, flag = 0; 30 for(i = 1; i <= G->vexNum; i++) 31 { 32 for(j = 1; j <= G->vexNum; j++) 33 { 34 if(G->vex[i][j] != MAX_VALUE) 35 { 36 flag ++; 37 break; 38 } 39 } 40 } 41 if(flag < G->vexNum) 42 return 0; 43 else 44 return 1; 45 } 46 47 void print(Graph *G) 48 { 49 int i, j; 50 for(i = 1; i <= G->vexNum; i++) 51 { 52 for(j = 1; j <= G->vexNum; j++) 53 printf("%d ", G->vex[i][j]); 54 printf("\n"); 55 } 56 } 57 58 int Min(Graph *G, struct closedeg cld[]) 59 { 60 int i, min = MAX_VALUE, min_index = 2; 61 for(i = 2; i <= G->vexNum; i++) 62 { 63 if(cld[i].lowcost != 0) 64 { 65 if(min > cld[i].lowcost) 66 { 67 min = cld[i].lowcost; 68 min_index = i; 69 } 70 } 71 } 72 return min_index; 73 } 74 75 void Prim(Graph *G, int v) 76 { 77 int i, e; 78 int k0, u0, v0; 79 int sum = 0; 80 closedeg[v].lowcost = 0; 81 for(i = 1; i <= G->vexNum; i++) //对V-U中的点进行初始化closedeg[] 82 { 83 if(i != v) 84 { 85 closedeg[i].vex = v; 86 closedeg[i].lowcost = G->vex[v][i]; 87 } 88 } 89 90 for(e = 1; e <= G->vexNum - 1; e++) //找到n-1条边 91 { 92 93 k0 = Min(G, closedeg); 94 u0 = closedeg[k0].vex; //最小边的点左端点 95 v0 = k0; //最小边的点右端点 96 // printf("(%d, %d) \n", u0, v0);; //输出最小边 97 sum += G->vex[u0][v0]; 98 closedeg[k0].lowcost = 0; 99 for(i = 2; i <= G->vexNum; i++) 100 { 101 if(G->vex[k0][i] < closedeg[i].lowcost) 102 { 103 closedeg[i].lowcost = G->vex[k0][i]; 104 closedeg[i].vex = v0; 105 } 106 } 107 } 108 if(1 == isLianTong(G)) 109 printf("%d\n", sum); 110 else 111 printf("-1\n"); 112 } 113 114 void creat(Graph *G) 115 { 116 int i; 117 // FILE *fp; 118 // fp = fopen("input.txt", "r"); 119 scanf("%d %d", &G->vexNum, &G->arsNum); 120 // fscanf(fp, "%d %d", &G->vexNum, &G->arsNum); 121 init(G); 122 for(i = 1; i <= G->arsNum; i++) 123 { 124 int ars1, ars2, weight; 125 scanf("%d %d %d", &ars1, &ars2, &weight); 126 // fscanf(fp, "%d %d %d", &ars1, &ars2, &weight); 127 G->vex[ars1][ars2] = weight; 128 G->vex[ars2][ars1] = weight; 129 } 130 // print(G); 131 } 132 133 int main() 134 { 135 Graph G; 136 creat(&G); 137 Prim(&G, 1); 138 return 0; 139 }
这里面有很多函数是这个题目所不需要的。因为我在写这个程序的时候并不是一帆风顺的,中间遇到过很多问题。所以保留了一些我改动的痕迹。
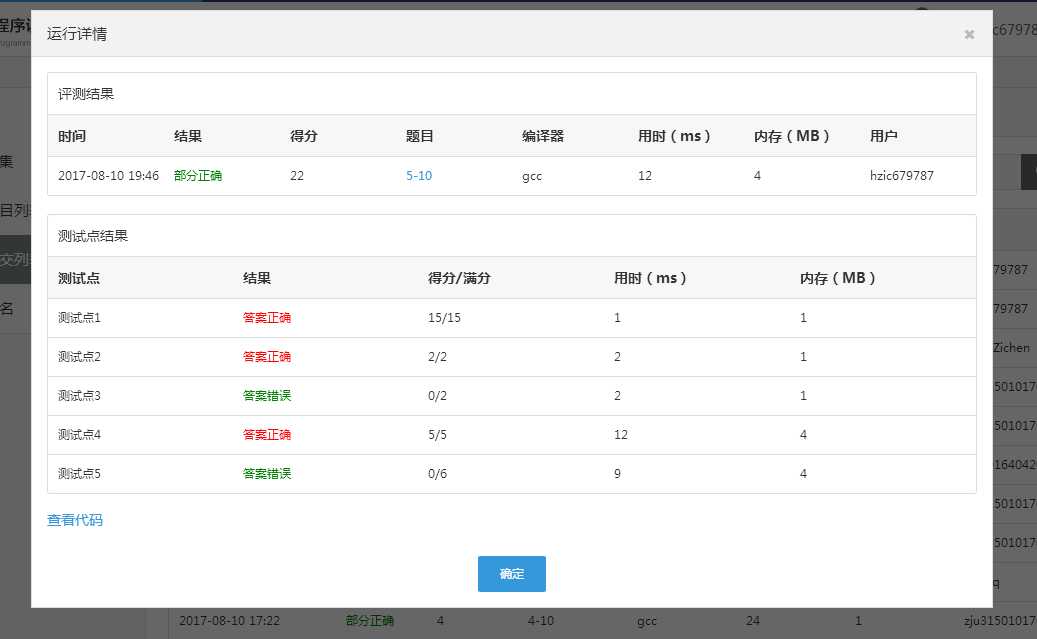
只可惜最后上传的时候只能拿22分,剩下还有两个测试点,我也不知道哪个地方出了问题。