标签：nes and 技术分享 有关 笛卡尔 randn 方法 信息 领域
目的： 实现6种（2ASK、4ASK、2FSK、4FSK、2PSK、4PSK）调制信号自动调制识别。
条件：windows 10，MATLAB 2014a
内容： 本实验设计了一个分层结构的MLP神经网络分类器。该分类器使用BP算法，自适应改变判决门限，6种调制信号的整体平均识别率为96.94。
更多内容查看：word版（内附完整源代码）下载地址：http://download.csdn.net/download/lanluyug/9923631
振幅键控，就是根据基带信号改变载波的幅度。最简单的实现方式是载波的频率不变，使用二进制信号“0”和“1”控制。2ASK信号可以表示成一个单极性矩形脉冲序列与一个正弦波相乘，其时域表达式为:
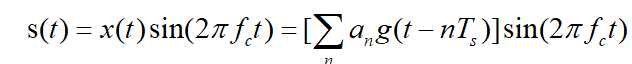
其中matlab代码实现2ASK为：
% 2ASK signal
x=randint(1,M); %M为64，x为随机生成的1*64的随机矩阵（矩阵元素由0和1组成）
m=sin(2*pi*fc*t); %载波信号
y=ones(1,M*N); %M=64,N=200,y为1*12800的全1矩阵
for i=1:M
for j=1:N
y((i-1)*N+j)=x(i)*m(j); %随机生成的2ASK信号
end
end
原理：使用randint()函数生成1*M的随机矩阵（此矩阵由0和1两种元素组成）；此时矩阵x=randint()可充当单极性矩形脉冲序列，最后两层嵌套循环生成2ASK信号：y((i-1)*N+j)=x(i)*m(j);
频移键控，就是根据基带信号改变载波的频率。二进制频移键控，是指调制信号“0”和“1”分别对应载波的两个频率f1和f2。此时2FSK信号可以看成调整幅度为0和1的两个2ASK信号的叠加，其时域表达式为：
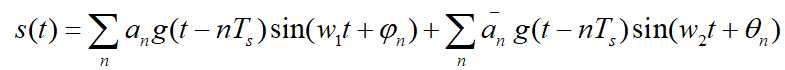
式子中g(t)为单个矩阵脉冲，脉宽为Ts
其中an取值如下：
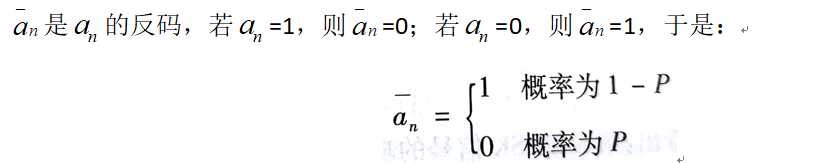
其中matlab代码实现2FSK为：
%2FSK signal
x=randint(1,M);
m1=sin(2*pi*fc*t); %载频信号1
m2=sin(2*pi*2*fc*t); %载频信号2
y=zeros(1,M*N);
for i=1:M
if x(i)==1;
for j=1:N;
y((i-1)*N+j)=x(i)*m1(j); %码元信息为1时，为m1频率波形
end
elseif x(i)==0;
for j=1:N;
y((i-1)*N+j)=(1-x(i))*m2(j); %码元信息为0时，为m2频率波形
end
end
end
原理：使用randint()函数生成1*M的随机矩阵（此矩阵由0和1两种元素组成）；此时矩阵x=randint()可充当单极性矩形脉冲序列，然后两层嵌套for循环加if判断x[i]生成两类2ASK信号，最后叠加成2FSK信号：x[i]=1时，y((i-1)*N+j)=x(i)*m1(j); x[i]=0时，y((i-1)*N+j)=(1-x(i))*m2(j)。
二进制相移键控（2PSK）是载波的相位随着二进制数字基带信号而变化，而振幅和频率保持不变。2PSK信号的时域表达式为：
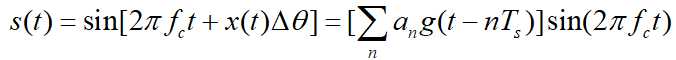
式子中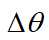
是相移常数，式子中是基带序列为“0”和“1”控制。
%2PSK signal,
x=randint(1,M);
m1=sin(2*pi*fc*t);
m2=sin(2*pi*fc*t+pi);
y=zeros(1,M*N);
for i=1:M
if x(i)==1;
for j=1:N;
y((i-1)*N+j)=x(i)*m1(j);
end
elseif x(i)==0;
for j=1:N;
y((i-1)*N+j)=(1-x(i))*m2(j);
end
end
end
原理：使用randint()函数生成1*M的随机矩阵（此矩阵由0和1两种元素组成）；此时矩阵x=randint()可充当单极性矩形脉冲序列，然后两层嵌套for循环加if判断x[i]生成两类相位相差π的2ASK信号，最后叠加成2PSK信号：当x[i]=1时，m1=sin(2*pi*fc*t); y((i-1)*N+j)=x(i)*m1(j); 当x[i]=0时，m2=sin(2*pi*fc*t+pi);
y((i-1)*N+j)=(1-x(i))*m2(j)。
4ASK,4FSK,4PSK调制信号matlab代码采用类似手段构成，在此不作介绍，详细信息可以参考最后附录的源代码。再者，本次实验设置参数如下：载波频率fc=20000；采样频率fs=40000；信息码元长度=15*round(k*fs/fc); 信号长度t0=5.5; 采样点个数Ns=256; 符号速率fd=200; 码元个数M=64，信噪比SNR=5dB;更多细节可参考附录源代码，本人在多数代码后面都写有注释。
目前，自动调制识别方法可以分为两大类：统计判决理论方法和统计模式识别方法。本次报告词用后者。
一个通用的模式识别系统由信号预处理、特征提取和分类识别三部分组成。根据识别部分采用不同又可以分为基于决策理论的信号调制识别、基于人工神经网络的信号调制识别和基于支持向量机的信号调制识别。下图为自动调制识别一般流程：
E.E.Azzouz和A.K.Nandi发表多篇调制信号识别的类似文章，利用他们提出的五个参数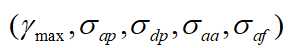
，采用判决数的方法对数字信号集（2ASK、4ASK、2FSK、4FSK、2PSK、4PSK）进行识别分类，在信噪比10dB时，识别率高于90%，在信噪比为20dB时，识别率高于96%。
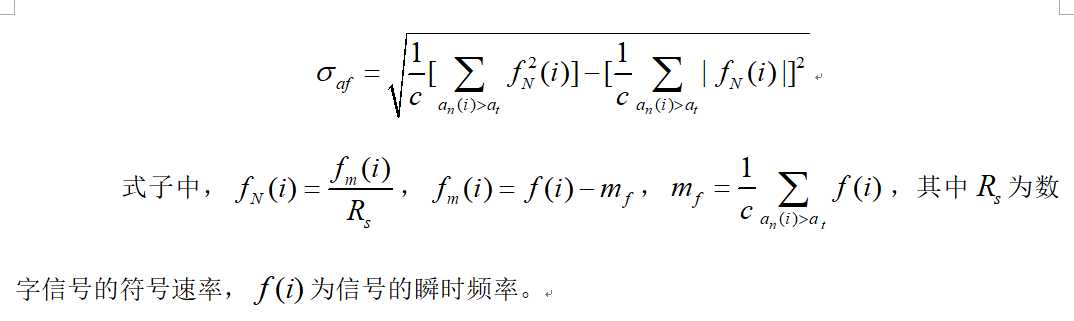
人工神经网络（ANN）是仿生物神经网络的结构提出的，他是由大量简单的计算单元（节点）相互连接而构成的一种并行分布式处理网络。神经网络的分布处理以及它所特有的高度容错性、自组织和自学习能力使它在自动调制识别领域具有很强的应用能力。
神经网络分类器一般由许多个计算节点组成，每个节点只有一个输出，而这个输出可以连接很多其他的计算节点，每个节点的输入有很多个连接通路，每个连接通路对应于一个连接权系数。
（1） 每个节点具有一个状态变量；
（2） 节点i到节点j有一个权系数；
（3） 每个节点有一个阈值；
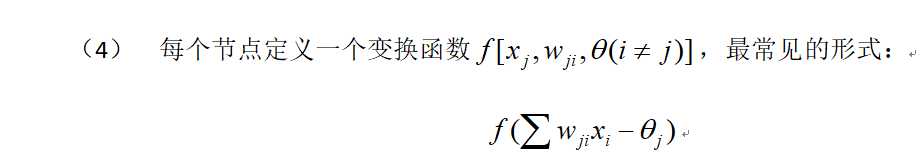
在通信信号自动调制识别应用中，一般选用基于有监督训练的神经网络模型作为分类器，特别是各种有监督训练的前馈神经网络，其中的MLP（多层感知器）和RBF（径向基函数神经网络）是最常用的两种模型。
（1）隐含层数的选择
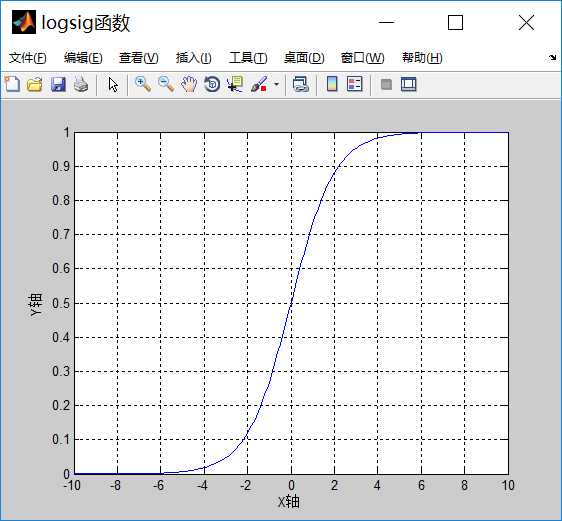
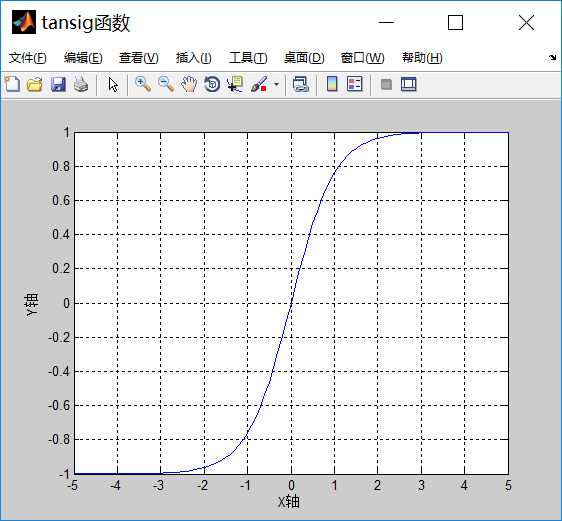
本文设计的神经网络分类器是一个具有三层网络结构的神经网络分类器：输入层、一个隐藏层和输出层。输入层到隐含层采用的传递函数（激活函数）是S型对数函数logsig，隐含层到输出层采用的传递函数是S型正切函数tansig。
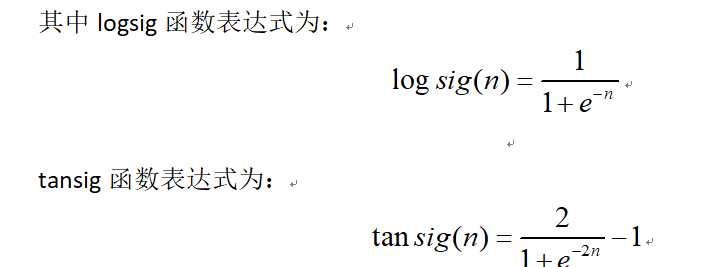
两个函数的笛卡尔坐标图分别为：
（2）隐含层节点数的确定
由于ANN是一个极为复杂的非线性动态系统，因此很难找到有关其特征、容量一类的简洁解析表达式，常用的一个确定隐含层节点的方法为试凑法：先设置较少的隐含节点训练网络，然后逐渐增加隐含点，用同一样本集进行训练，从中确定网络误差最小时对应的隐节点数。在用试凑法时，可以用一些确定的隐节点数的经验公式。
ANN最常见的试凑法的经验公式如下：
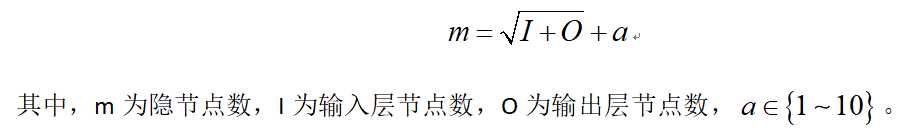
（3）训练样本集与测试样本集
6种（2ASK、4ASK、2FSK、4FSK、2PSK、4PSK）调制信号的目标结果以1，2，3，4，5，6来表示。本文选取的训练样本集包含了这六种调制信号的特征参数向量各200组，测试样本集为包含了这6种调制信号特征参数向量各60组。
% 6种（2ASK、4ASK、2FSK、4FSK、2PSK、4PSK）调制信号的自动调制识别matlab2014a
clear all;
close all;
echo off; %神经网络训练时不显示每一步的梯度和误差性能
fc=20000; %载波频率
fs=40000; %采样速率
k=2; %常用系数k为2
code_size=15*round(k*fs/fc); %信息码元长度
t0=5.5; %信号长度
Ns=256; %采样点个数
fd=200; %符号速率
ts=1/fs; %采样周期
M=64 %码元个数
ti=1/fd; %码元间隔 N=200
N=ti/ts
t=[0:ts:t0];
select=menu(‘调制方式‘,‘2ASK‘,‘2FSK‘,‘2PSK‘,‘4ASK‘,‘4FSK‘,‘4PSK‘);
switch select
case 1, % 2ASK signal
x=randint(1,M); %M为64，x为随机生成的1*64的随机矩阵（矩阵元素由0和1组成）
m=sin(2*pi*fc*t); %载波信号
y=ones(1,M*N); %M=64,N=200,y为1*12800的全1矩阵
for i=1:M
for j=1:N
y((i-1)*N+j)=x(i)*m(j); %随机生成的2ASK信号
end
end
T=zeros(6,50); %T为6*50的全0矩阵
T(1,1:50)=1; %将矩阵T第一行全部置1
case 2, %2FSK signal
x=randint(1,M);
m1=sin(2*pi*fc*t); %载频信号1
m2=sin(2*pi*2*fc*t); %载频信号2
y=zeros(1,M*N);
for i=1:M
if x(i)==1;
for j=1:N;
y((i-1)*N+j)=x(i)*m1(j); %码元信息为1时，为m1频率波形
end
elseif x(i)==0;
for j=1:N;
y((i-1)*N+j)=(1-x(i))*m2(j); %码元信息为0时，为m2频率波形
end
end
end
T=zeros(6,50);
T(2,1:50)=1;
case 3, %2PSK signal,
x=randint(1,M);
m1=sin(2*pi*fc*t);
m2=sin(2*pi*fc*t+pi);
y=zeros(1,M*N);
for i=1:M
if x(i)==1;
for j=1:N;
y((i-1)*N+j)=x(i)*m1(j);
end
elseif x(i)==0;
for j=1:N;
y((i-1)*N+j)=(1-x(i))*m2(j);
end
end
end
T=zeros(6,50);
T(3,1:50)=1;
case 4, % 4ASK signal
x=randint(1,M,4);
m=sin(2*pi*fc*t);
y=ones(1,M*N);
for i=1:M
if x(i)==0;
for j=1:N
y((i-1)*N+j)=x(i)*m(j);
end
elseif x(i)==1;
for j=1:N
y((i-1)*N+j)=x(i)*m(j);
end
elseif x(i)==2;
for j=1:N
y((i-1)*N+j)=x(i)*m(j);
end
elseif x(i)==3;
for j=1:N
y((i-1)*N+j)=x(i)*m(j);
end
end
end
T=zeros(6,50);
T(4,1:50)=1;
case 5, % 4FSK signal
x=randint(1,M,4);
m1=sin(2*pi*fc*t);
m2=sin(2*pi*2*fc*t);
m3=sin(2*pi*3*fc*t);
m4=sin(2*pi*4*fc*t);
y=zeros(1,M*N);
for i=1:M
if x(i)==0;
for j=1:N
y((i-1)*N+j)=(1-x(i))*m1(j);
end
elseif x(i)==1;
for j=1:N
y((i-1)*N+j)=x(i)*m2(j);
end
elseif x(i)==2;
for j=1:N
y((i-1)*N+j)=(x(i)-1)*m3(j);
end
elseif x(i)==3;
for j=1:N
y((i-1)*N+j)=(x(i)-2)*m4(j);
end
end
end
plot(y)
T=zeros(6,50);
T(5,1:50)=1;
case 6, %4PSK signal
x=randint(1,M,4);
m1=sin(2*pi*fc*t);
m2=sin(2*pi*fc*t+pi/2);
m3=sin(2*pi*fc*t+pi);
m4=sin(2*pi*fc*t+3*pi/2);
y=zeros(1,M*N);
for i=1:M
if x(i)==0;
for j=1:N
y((i-1)*N+j)=(1-x(i))*m1(j);
end
elseif x(i)==1;
for j=1:N
y((i-1)*N+j)=x(i)*m2(j);
end
elseif x(i)==2;
for j=1:N
y((i-1)*N+j)=(x(i)-1)*m3(j);
end
elseif x(i)==3;
for j=1:N
y((i-1)*N+j)=(x(i)-2)*m4(j);
end
end
end
T=zeros(6,50);
T(6,1:50)=1;
end
SNR=5; %定义信噪比，单位dB
sigpow=mean(abs(y).^2); %power of input signal
noisefac=10^(-SNR/10);
noise=randn(1,size(y,2));
noise=noise*(sqrt(sigpow*noisefac)/sqrt(mean(noise.^2))); %产生所需的高斯噪声
ynoise=noise+y; %加噪后的信号
for n=1:1:50
m=n*Ns;
x=(n-1)*Ns;
for i=x+1:m; %提取信号段
y0(i)=ynoise(i);
end
Y=fft(y0); %调制信号的傅立叶变换
y1=hilbert(y0); %实信号的解析式
z=abs(y0); %实信号的瞬时幅度
phase=angle(y1); %实信号的瞬时相位
add=0; %求Rmax
for i=x+1:m;
add=add+z(i);
end
ma=add/Ns; %瞬时幅度的平均值
y2=z./ma ; %幅度比,即为文献中的an(i)
y2n=y2-1; %归一化瞬时幅度
Rmax=max(abs(fft(y2n.^2)/Ns));%零中心归一化瞬时幅度的谱密度的最大值
Xcn=0;
Ycn=0;
for i=x+1:m;
Xcn=Xcn+y2n(i).*y2n(i);
Ycn=Ycn+abs(y2n(i));
end
Xcnav=Xcn/Ns;
Ycnav=(Ycn/Ns).*(Ycn/Ns);
deltaaa=sqrt(Xcnav-Ycnav); %零中心归一化瞬时幅度绝对值得标准偏差
if phase(2+x)-phase(1+x)>pi; %修正相位序列
Ck(1+x)=-2*pi;
elseif phase(1+x)-phase(2+x)>pi;
Ck(1+x)=2*pi;
else Ck(1+x)=0;
end
for i=x+2:m-1;
if phase(i+1)-phase(i)>pi;
Ck(i)=Ck(i-1)-2*pi;
elseif phase(i)-phase(i+1)>pi
Ck(i)=Ck(i-1)+2*pi;
else
Ck(i)=Ck(i-1);
end
end
if -phase(m)>pi;
Ck(m)=Ck(m-1)-2*pi;
elseif phase(m)>pi;
Ck(m)=Ck(m-1)+2*pi;
else Ck(m)=Ck(m-1);
end
phase1=phase+Ck %去相位卷叠后的相位序列
phasenl=phase1-2*pi*fc*i/fs; %非线性相位
at=1; %判决门限电平
a=0; %求取零中心非弱信号段瞬时相位非线性分量绝对值的标准偏差和零中心非弱信号段瞬时相位非线性分量的标准偏差
b=0;
d=0;
c=0;
for i=x+1:m;
if y2(i)>at
c=c+1;
phasesquare(i)=phasenl(i).*phasenl(i);
a=a+phasesquare(i);
phaseabs(i)=abs(phasenl(i));
b=b+phaseabs(i);
d=d+phasenl(i)
end
end
a1=a/c;
b1=(b/c).*(b/c);
d1=(d/c).*(d/c);
deltaap=sqrt(a1-b1); %零中心非弱信号段瞬时相位非线性分量绝对值的标准偏差
deltadp=sqrt(a1-d1); %零中心非弱信号段瞬时相位非线性分量的标准偏差
freqN(i)=phase1(i)-phase1(i-1);
for i=x+1:m;
if i>at;
c=c+1;
freqNsquare(i)=freqN(i).*freqN(i);
a=a+freqNsquare(i);
b=b+freqN(i);
end
end
a1=a/c;
b1=(b/c)^2;
deltaaf=sqrt(a1-b1); %零中心归一化非弱信号段瞬时频率绝对值得标准偏差
Pi=rand(5,50);
P0=rand(5,50);
Pi(5*n-4)=Rmax;
Pi(5*n-3)=deltaap;
Pi(5*n-2)=deltadp;
Pi(5*n-1)=deltaaa;
Pi(5*n)=deltaaf;
end
%采用BP网络
%NEWCF--生成一个新的前向神经网络
%TRAIN--对网络进行训练
% 定义训练样本
%Pi为输入矢量
%T为目标矢量
%创建一个新的前向神经网络
net=newff(minmax(Pi),[5,15,6],{‘tansig‘,‘purelin‘,‘logsig‘},‘traingda‘);
%设置训练参数
net.trainParam.show=50; %两次显示之间的训练步数
net.trainParam.lr=1; %
net.trainParam.mc=0.5;
net.trainParam.epochs=2000; %训练次数
net.trainParam.goal=1e-3; %训练目标
%调用TRAINGDM算法训练网络
[net,tr]=train(net,Pi,T);
%对网络进行仿真
A=sim(net,Pi);
E=T-A;
T1=zeros(6,50);
T1(1,1:50)=1;
E1=0;
for c=1:1:300
Eout=(T1(c)-A(c))^2;
E1=Eout+E1 ;
end
T2=zeros(6,50);
T2(2,1:50)=1;
E2=0;
for c=1:1:300
Eout=(T2(c)-A(c))^2;
E2=Eout+E2;
end
T3=zeros(6,50);
T3(3,1:50)=1;
E3=0;
for c=1:1:300
Eout=(T3(c)-A(c))^2;
E3=Eout+E3;
end
T4=zeros(6,50);
T4(4,1:50)=1;
E4=0;
for c=1:1:300
Eout=(T4(c)-A(c))^2;
E4=Eout+E4;
end
T5=zeros(6,50);
T5(5,1:50)=1;
E5=0;
for c=1:1:300
Eout=(T5(c)-A(c))^2;
E5=Eout+E5;
end
T6=zeros(6,50);
T6(6,1:50)=1;
E6=0;
for c=1:1:300
Eout=(T6(c)-A(c))^2;
E6=Eout+E6;
end
E0=0;
if (E1>E2)
E0=E2;
else E0=E1;
end
if (E3<E0)
E0=E3;
end
if (E4<E0)
E0=E4;
end
if (E5<E0)
E0=E5;
end
if (E6<E0)
E0=E6;
end
E0;
if (E0==E1)
type=menu(‘输入信号是‘,‘2ASK信号‘);
end
if (E0==E2)
type=menu(‘输入信号是‘,‘2FSK信号‘);
end
if(E0==E3)
type=menu(‘输入信号是‘,‘2PSK信号‘);
end
if(E0==E4)
type=menu(‘输入信号是‘,‘4ASK信号‘);
end
if(E0==E5)
type=menu(‘输入信号是‘,‘4FSK信号‘);
end
if(E0==E6)
type=menu(‘输入信号是‘,‘4PSK信号‘);
end
%计算正确识别率sita
sita=0;
j=0;
for nn=1:1:50
Ee=(E(6*nn-5)^2)+(E(6*nn-4)^2)+(E(6*nn-3)^2)+(E(6*nn-2)^2)+(E(6*nn-1)^2)+(E(6*nn)^2);
if Ee<0.01
j=j+1
end
end
sita=j/50;
type=menu(‘正确识别率为:‘,sita*100,‘％‘)
基于ANN的6种调制信号自动调制识别（2ASK、4ASK、2FSK、4FSK、2PSK、4PSK）
标签：nes and 技术分享 有关 笛卡尔 randn 方法 信息 领域
原文地址：http://www.cnblogs.com/lanluyug/p/7346555.html
