标签:get -- ever 考试 ges color 今天 技术 评测

样例输入:
3 6
0 -1 1
1 0 -1
-1 1 0
1 2 3 1 2 3
样例输出:
3

题解
不要看上面那个吓人的时间限制……实际上内网给了4Sec,高明的模拟能过;外网给的时间比这还多,直接暴力模拟就能A,这就是为什么我今天成绩莫名高了不少。刚开始就只想到了模拟,用链表可以稍微优化一点有限,然而时间效率近似于n*答案,要依靠答案的大小来决定时间效率,让我不由得想到某名为《天鹅会面》的惨痛事故。想了很久还是没想出来,直接把模拟当做骗分程序来写,连快读都没有写;自认为是今天最不靠谱的一个程序。曾经想过每次至少有一个钟会破产,可以依据这个优化一下,但是当时没有想到应该怎么维护财产,觉得优化之后反而不准确就干脆没有改。竞赛到时间之后一刷新……诶……这道题居然A了?!我打的不是暴力无剪枝模拟吗?然后第一次觉得外网评测机好像跑得还不算太慢。交到内网按测试点计时,最后一个点过不了。ryf大佬的方法在普通模拟的基础上每次把一个钟破产的最早时间作为单位时间,节省了很多冗余的步骤,速度快到飞起,优化之后在内网也轻松过掉。题解上提到可以证明至多在3*n秒内会终止,这大约也是模拟可行的重要依据。然而应该怎样证明呢?并不是很清楚,在考场上做一个这种级别的证明大概也是不值得的吧。

#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int sj=1000005; int c,n,cl[sj],ft[105][105],cc[sj],cz[105],zls; int pr[sj],nt[sj],zq,ss[sj]; bool wd; inline int r(){ int s=0,k=1;char ch=getchar(); while(ch<48||ch>‘9‘) k=(ch==‘-‘)?-1:k,ch=getchar(); while(ch>47&&ch<=‘9‘)s=s*10+(48^ch),ch=getchar(); return s*k; } void bj(int &x,int y) { x=x<y?x:y; } int main() { c=r(); n=r(); for(int i=1;i<=c;i++) { wd=1; for(int j=1;j<=c;j++) { scanf("%d",&ft[i][j]); if(ft[i][j]<0) wd=0; } if(wd) { printf("%d",i); return 0; } } for(int i=1;i<=n;i++) { cl[i]=r(),cc[i]=1; pr[i]=i-1,nt[i]=i+1; if(cz[cl[i]]==0) zls++; cz[cl[i]]++; } nt[0]=1,nt[n]=0; while(zls!=1) { zq=0x7fffffff; for(int i=nt[0];i;i=nt[i]) { ss[i]=0; if(pr[i]) ss[i]+=ft[cl[i]][cl[pr[i]]]; if(nt[i]) ss[i]+=ft[cl[i]][cl[nt[i]]]; if(ss[i]<0) bj(zq,(cc[i]-1)/(-ss[i])+1); } for(int i=nt[0];i;i=nt[i]) cc[i]+=zq*ss[i]; for(int i=nt[0];i;i=nt[i]) if(cc[i]<=0) { cz[cl[i]]--; if(cz[cl[i]]==0) zls--; pr[nt[i]]=pr[i]; nt[pr[i]]=nt[i]; } } for(int i=0;i!=n+1;i=nt[i]) if(i!=0) { printf("%d",cl[i]); break; } return 0; }

2.4 样例输入输出
样例输入:
4 4 4
1 2 1
2 3 3
3 4 2
4 1 4
3 2
3 3
3 1
3 4
样例输出:
2
4
1
4
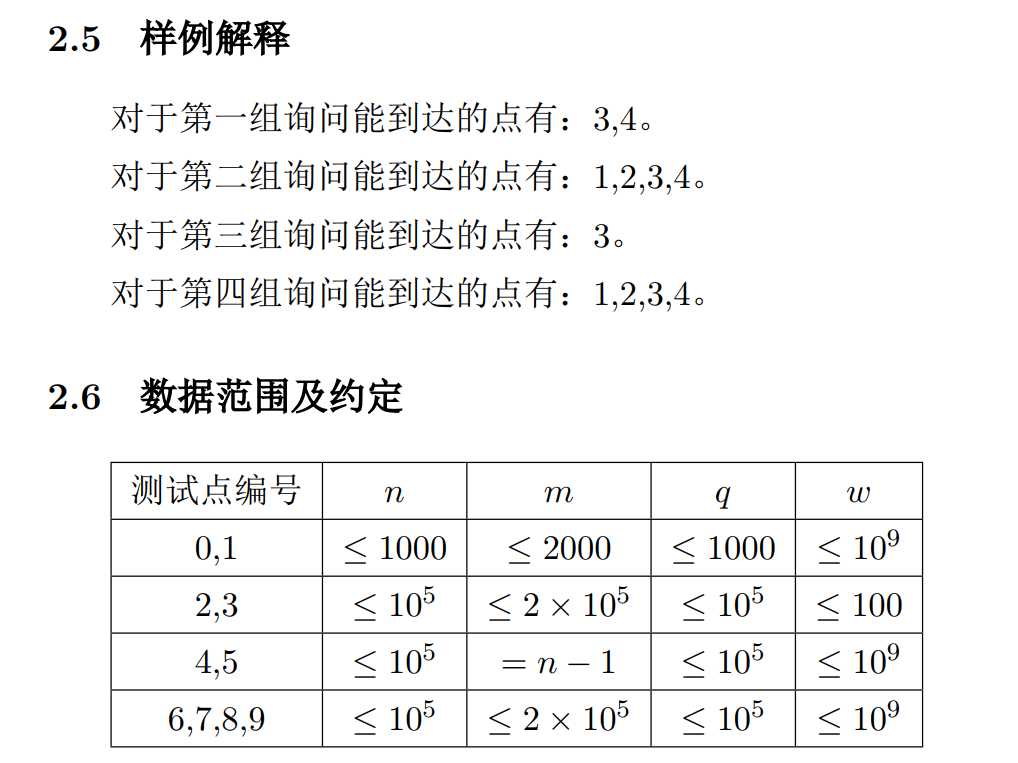
题解
题干很简单,但是解决也不是那么容易。刚开始非常直接地打了个dfs暴力查询,大概只能拿20分。受到测试点的启发,树是比较容易的图形,然后想到了最小生成树。图不算特别稠密,不是必须要用普里姆,不花什么力气就打出了克鲁斯卡尔。然而这样只不过是把一次dfs的复杂度上限从2*m降到了n,并没有优化太多,想要拿比20更多的分还是很没底。如果预处理到每点的最大边权,时间和空间复杂度都承受不了。从图到树,难道还要从树到链吗?但是想了想树链剖分感觉并不靠谱。到最后都没有想出正解,交上了20分的程序。
正解是在克鲁斯卡尔过程中维护并查集(或者用一些叫做克鲁斯卡尔重构树的神奇东西?)。虽然图上的边和询问看起来完全不是一种东西,它们却都有对边权的要求。曾经想过对每一个询问中的w生成一棵树,然而问题在于时间复杂度太高也未必真能生成一棵完整的树。但是如果把询问像图上的边一样记录下来,在克鲁斯卡尔给边排序时一同排序,就可以在生成树的过程中机智无比地解决问题了。克鲁斯卡尔对于树的鉴定是通过并查集实现的,我们在这里也用并查集,甚至不用真正构建生成树,只要把集合大小作为附加信息维护就可以了,集合的大小正是把当前边权作为最大边权所能到达的点数。唯一的一点细节是当边权与询问的w相同时先加边再询问。正所谓四两拨千斤,喜欢并查集的最主要原因 就是它能用非常巧妙的方法解决看似复杂的问题,思维转化的过程又妙趣横生,维护附加信息的操作更是让人拍案叫绝。如果下次我能用并查集A一道题,一定会非常高兴的。

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int sj=100005; int n,m,q,a1,a2,a3,e2,l[sj],fa[sj],size[sj],ans[sj]; struct yb { int ne,w,v,u,lx; }c[sj*6]; void ad2(int x,int y,int z,int op) { c[e2].v=y; c[e2].u=x; c[e2].w=z; c[e2].lx=op; c[e2].ne=l[x]; l[x]=e2++; } int comp(const yb&a,const yb&b) { return (a.w==b.w)?(a.lx>b.lx):(a.w<b.w); } int find(int x) { if(fa[x]==x) return x; fa[x]=find(fa[x]); return fa[x]; } void hb(int x,int y) { x=find(x),y=find(y); if(x!=y) fa[x]=y; size[y]+=size[x]; } int main() { scanf("%d%d%d",&n,&m,&q); memset(l,-1,sizeof(l)); for(int i=1;i<=m;i++) { scanf("%d%d%d",&a1,&a2,&a3); ad2(a1,a2,a3,1); ad2(a2,a1,a3,1); } for(int i=1;i<=n;i++) fa[i]=i,size[i]=1; for(int i=1;i<=q;i++) { scanf("%d%d",&a1,&a2); ad2(a1,i,a2,0); } sort(c+0,c+e2,comp); for(int i=0;i<e2;i++) { if(c[i].lx==1) if(find(c[i].v)!=find(c[i].u)) hb(c[i].u,c[i].v); if(c[i].lx==0) ans[c[i].v]=size[find(c[i].u)]; } for(int i=1;i<=q;i++) printf("%d\n",ans[i]); return 0; }
区间第K大(kth)
出题人:任路遥
时间限制:2s 空间限制:256MB
【题目描述】
想必大家对区间第K大问题相当熟悉了。这个问题是这样的,给一串序列和若干询问,每个询问查询某段连续区间中第K大的数。现在我们考虑一个该问题的“Reverse”版本。现在我们给出序列和Q个询问,每个询问给出K_i和X_i,询问有多少区间其第K_i大的数为X_i。
【输入说明】
第一行一个整数N和Q,表示序列长度和询问个数。
第二行N个整数A_i,表示序列中的元素。
接下来Q行,每行两个整数K_i和X_i,表示询问。
【输出说明】
一共Q行,每行表示对应询问的答案。
【样例输入】
3 2
1 1 2
1 1
2 1
【样例输出】
3
3
【数据范围】
对于20%的数据,N<=100
对于40%的数据,N<=500
对于100%的数据,N<=2000,Q<=2000000, 1 ≤ K_i ≤ N,1 ≤ X_i ≤ N
【题解】
刚开始的时候打算先打个不管不顾的暴力,什么时间复杂度都行。后来看了看询问数2*10^6,而且还不分层,在它的基础上乘上什么都很难不超时啊,所以说这题离线或者预处理算是稳了吧。预处理比较好打,毕竟n和k的范围都只有2000,直接n^3枚举和遍历区间,加上每次快排的logn,40分拿得还是比较稳。然而用这种思路来做实在是没有优化空间,区间枚举少一点答案就会不准确,果然正解用的是一种截然不同的思路。
回忆一下前天T1calc,那道顺序对的题,一个数对答案的贡献取决于前后和它有某种特殊关系的数的数量。这道题也是一样,一个数在区间里第k大不就是说明有k-1个数比它更大吗?对于每一个数枚举它左右比它大的所有数的位置,只要在一个比它大的数一侧,又没有到下一个数,这一段里的点都可以作区间的一个端点。根据乘法计数原理,两边可行的端点数相乘就是可行答案数。左边取到的数越来越少,就要求右边取到的越来越多,只要满足左+右=k-1即可。对于序列中的每一个数枚举它所在区间的的左侧端点右侧端点,不到n^3的效率就能得出所有答案,最后o(1)查询。计算左边的时候等号可取,右边则不取,可以有效地避免重复计数。
正解确实很巧妙,可是毕竟做过calc,本该想到的。一个类型的题总是要多做几遍才能形成思路,然而最有效的方法大概是考试丢分吧(笑),自从那次考试前缀和没想到丢了几十分之后做题再也不会完全想不起前缀和了~

#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int sj=2005; int f[sj][sj],a[sj],n,a1,a2,q[sj],h[sj],qi; int main() { scanf("%d%d",&n,&qi); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=1;i<=n;i++) { a1=a2=0; for(int j=i-1;j>0;j--) if(a[i]<=a[j]) q[++a1]=j; q[a1+1]=0; for(int j=i+1;j<=n;j++) if(a[j]>a[i]) h[++a2]=j; h[a2+1]=n+1; q[0]=h[0]=i; for(int j=0;j<=a1;j++) for(int k=0;k<=a2;k++) f[a[i]][j+k+1]+=(q[j]-q[j+1])*(h[k+1]-h[k]); } for(int i=1;i<=qi;i++) { scanf("%d%d",&a1,&a2); printf("%d\n",f[a2][a1]); } return 0; }
标签:get -- ever 考试 ges color 今天 技术 评测
原文地址:http://www.cnblogs.com/moyiii-/p/7347649.html