网络流

标签：多少   技术   strong   span   log   条件   有向图   完整   工厂   

一、网络流

一个有向图满足一定的条件后就可称为网络流图。

如下面的有向图就是一个网络流图：

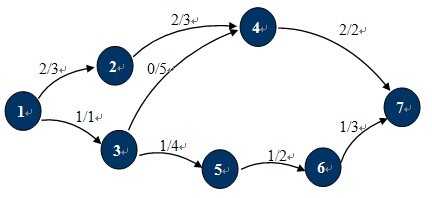
由图可知，网络流相较于有向图的特征为：

• 有唯一的源点S
• 有唯一的汇点T
• 每条弧都有一非负容量c[u][v]

也就是说，只要一个有向图有上面3个特征，这个图就是网络流。

二、网络流的性质

1. 每条弧上有两个量，即容量c[u][v]和流量f[u][v]，且满足f[u][v]<=c[u][v]；
   
2. 若容量c[u][v]==0，则说明弧<u,v>不存在；
3. 除点S和点T外，其余点的流入量==流出量 。

【联系实际解释网络流】

通常可以把这些边想象成道路，流量就是这条道路的车流量，容量就是道路可承受的最大的车流量。很显然的，流量<=容量。而对于每个不是源点和汇点的点来说，可以类比的想象成没有存储功能的货物的中转站，所有“进入”他们的流量和等于所有从他本身“出去”的流量。

三、可行流

• 每条弧上都给定一个实数f[u][v]作为这条弧上的流量，且0 =< f[u][v] <= c[u][v]

可行流：指这样的一个流，它能从源点流到汇点。（间接的意思是，在弧的容量并不一定完整的情况下，这个流的流量不会超过它流到汇点所经过的任何一条弧的当时容量）

四、最大流

最大流：一个数值，表示从源点S到汇点T的最大流量。

举例示意：把源点比作工厂的话，最大流就是在不能超过道路的容量限制的前提下，能从工厂发出的最多货物。

最大流问题：求在满足网络流性质的情况下，从源点 s 到汇点 t 的最大流量。

举例示意：在不能超过道路的容量限制的前提下，求从工厂最多可以发出多少货物。

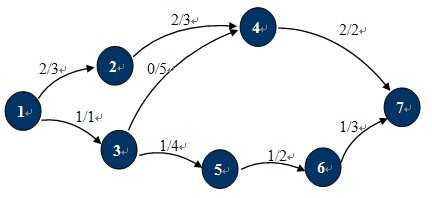
例：下面这个网络流的最大流为3 （每条弧上便是“流量/容量”）

网络流

标签：多少   技术   strong   span   log   条件   有向图   完整   工厂   

原文地址：http://www.cnblogs.com/xzxl/p/7348335.html