标签:赋值 scanf 组成 std 阴影 最大的 can 时间 手动
一个大的三角形,其中有向下的正三角形和向上的正三角形。求最大的正三角的组成人数(阴影部分不能算入)
这道题目卡了我好长时间,题目和之前做过的最大正方形有异曲同工之妙。只不过这道题目需要额外的处理一下。
首先我们看下向下的正三角如何求?
手动模拟会发现,和最大正方形类似。在i行j列的三角形的大小是受 (i-1,j) (i-1,j+1) (i-1,j-1) 这三个三角形的限制。这个我就不证明了。。
不过需要注意的是只有向下的三角形才能组成正三星形,这个怎么处理呢?每次记录Max值的之后判断一下这个三角形是不是向下的就可以了,如果不是就不用记录。
为什么?看着组数据
10
------------#####--
--#-----#-#--#---
--#----#---#---
-------#--#--
--#-#------
-----##--
---#---
-----
---
-
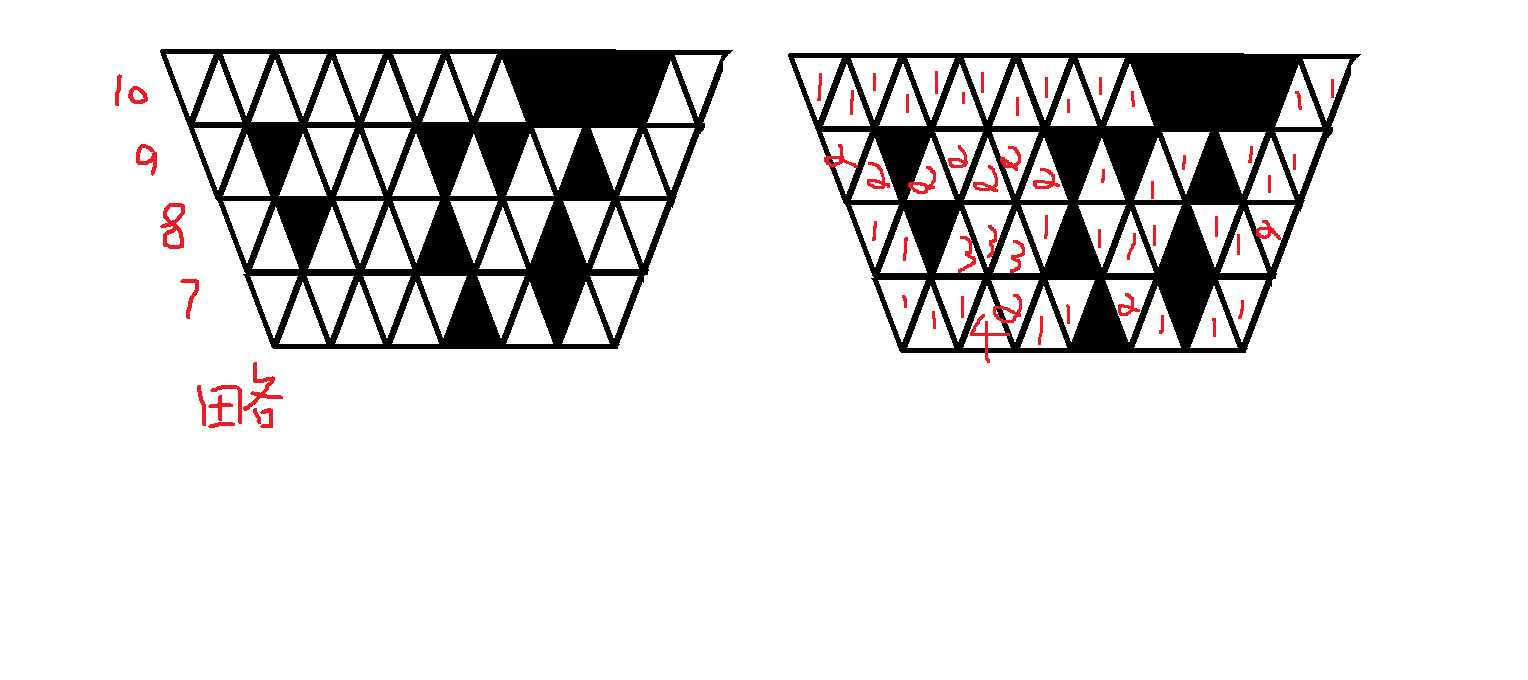
因为我们是在计算向下的三角形,所以不应该去考虑向上的三角形,但是不能忽略它的dp值,因为向上向下的三角形是一起参与构图的。
另一个同样方法。
代码实现
#include <cstdio> #include <cstring> #include <algorithm> int n,map[105][205],dp[105][205],Max=-1; char s[233]; int main(){ memset(dp,0,sizeof(dp)); memset(map,0,sizeof(map)); scanf("%d",&n); int pos = n*2+1; for(int i=1;i<=n;i++){ scanf("%s",s+1); for(int j=1;j<=pos-i*2;j++){ if(s[j]==‘-‘) map[i][j+i-1]=1; } } for(int i=1;i<=n;i++){ for(int j=i;j<=n*2-i;j++){ if(map[i][j]){ dp[i][j] = std::min(dp[i-1][j],std::min(dp[i-1][j+1],dp[i-1][j-1]))+1; if( (j-i+1)&1 )Max = std::max(dp[i][j],Max);//判断奇偶 } } } //记得赋值 memset(dp,0,sizeof(dp)); for(int i=n;i>=1;i--){ for(int j=i;j<=n*2-i;j++){ if(map[i][j]){ dp[i][j] = std::min(dp[i+1][j],std::min(dp[i+1][j+1],dp[i+1][j-1]))+1; if( !((j-i+1)&1) )Max = std::max(dp[i][j],Max);//偶数就判断 } } } //正三角形这个计算没啥说的 printf("%d\n",Max*Max); }
标签:赋值 scanf 组成 std 阴影 最大的 can 时间 手动
原文地址:http://www.cnblogs.com/OIerLYF/p/7351921.html