标签:can 失败 nod 说明 style 理解 malloc 变化 没有
一、相关介绍
知识要求
AC自动机
单模式串问题&多模式串问题
若我们暴力地用每一个模式串对主串做kmp,这样虽然理论上可行,但是时间复杂度非常之高。而AC自动机算法就能高效地处理这种多模式串问题。
二、算法实现
【打基础】
失配指针fail
假如我们有四个单词:abcd, bce, abd, cd,那么我们建立字典树如下:
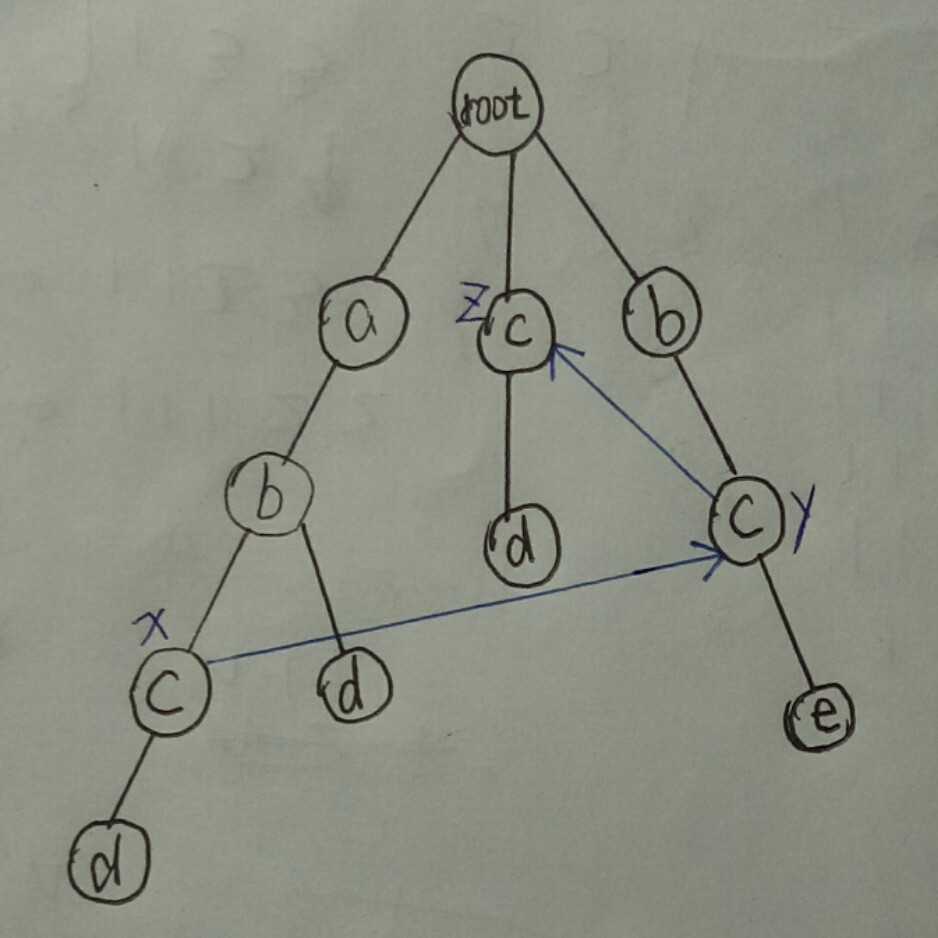
首先我们让与根节点直接相连的节点的fail直接指向root,为了让你更好的理解fail指针,我们以节点x,y,z为例,我们让从图中我们可以看出x节点的fail指向了y节点,y节点的fail指向了z节点,为什么会这样指,因为x节点表示字符串abc,而字典树中含有最长,且以c结尾,且是abc的后缀的字符串bc(以y节点结尾的),同理,以y节点表示的字符串是bc,而以c结尾,且是bc的后缀的最长字符串是c(以z节点结尾的)。这就是fail指针指向的目标,那么我们得到了这个fail指针在匹配中有什么用呢,我们还是用上面的那个图来举例说明一下,假设文本串是abce,通过字典树我们可以看出,通过abc,所以我们可以匹配到x节点,但是到后面,我们发现d与e不匹配,这时我们就需要用到当前节点的fail了,因为x的fail指向的是y节点,所以我们直接跳到y节点,这是发现y节点后面有e,匹配上了,所以单词bce就在文本串abce中被检测出来了。
【AC自动机简述】
【AC自动机的构造】
在建立字典树之前,我们先定义每个字典树上节点的结构体变量:
struct node{
node *next[26];
node *fail; //失配指针
int sum; //这个节点是不是一个单词的结尾,以及相应的个数。
};
建立字典树代码:
void Insert(char *s)
{
node *p = root;
for(int i = 0; s[i]; i++)
{
int x = s[i] - ‘a‘;
if(p->next[x] == NULL)
{
newnode=(struct node *)malloc(sizeof(struct node));
for(int j=0;j<26;j++) newnode->next[j] = 0;
newnode->sum = 0;newnode->fail = 0;
p->next[x]=newnode;
}
p = p->next[x];
}
p->sum++;
}
注意:在建立字典树的过程中,先让每个节点的fail指针先为空 。
下面是构造fail指针的具体代码(基于队列(bfs)实现):
void build_fail_pointer()
{
head = 0;
tail = 1;
q[head] = root;
node *p;
node *temp;
while(head < tail)
{
temp = q[head++];
for(int i = 0; i <= 25; i++)
{
if(temp->next[i])
{
if(temp == root)
{
temp->next[i]->fail = root;
}
else
{
p = temp->fail;
while(p)
{
if(p->next[i])
{
temp->next[i]->fail = p->next[i];
break;
}
p = p->fail;
}
if(p == NULL) temp->next[i]->fail = root;
}
q[tail++] = temp->next[i];
}
}
}
}
最后是利用前面求得的fail指针进行匹配。
代码如下:
void ac_automation(char *ch)
{
node *p = root;
int len = strlen(ch);
for(int i = 0; i < len; i++)
{
int x = ch[i] - ‘a‘;
while(!p->next[x] && p != root) p = p->fail;
p = p->next[x];
if(!p) p = root;
node *temp = p;
while(temp != root)
{
if(temp->sum >= 0)
{
cnt += temp->sum;
temp->sum = -1;
}
else break;
temp = temp->fail;
}
}
}
【AC自动机详讲】
我们给出5个单词,say,she,shr,he,her。给定字符串为yasherhs。问多少个单词在字符串中出现过。
一、Trie
首先我们需要建立一棵Trie。但是这棵Trie不是普通的Trie,而是带有一些特殊的性质。
首先会有3个重要的指针,分别为p, p->fail, temp。
1.指针p,指向当前匹配的字符。若p指向root,表示当前匹配的字符序列为空。(root是Trie入口,没有实际含义)。
2.指针p->fail,p的失败指针,指向与字符p相同的结点,若没有,则指向root。
3.指针temp,测试指针(自己命名的,容易理解!~),在建立fail指针时有寻找与p字符匹配的结点的作用,在扫描时作用最大,也最不好理解。
对于Trie树中的一个节点,对应一个序列s[1...m]。此时,p指向字符s[m]。若在下一个字符处失配,即p->next[s[m+1]] == NULL,则由失配指针跳到另一个节点(p->fail)处,该节点对应的序列为s[i...m]。若继续失配,则序列依次跳转直到序列为空或出现匹配。在此过程中,p的值一直在变化,但是p对应节点的字符没有发生变化。在此过程中,我们观察可知,最终求得得序列s则为最长公共后缀。另外,由于这个序列是从root开始到某一节点,则说明这个序列有可能是某些序列的前缀。
再次讨论p指针转移的意义。如果p指针在某一字符s[m+1]处失配(即p->next[s[m+1]] == NULL),则说明没有单词s[1...m+1]存在。此时,如果p的失配指针指向root,则说明当前序列的任意后缀不会是某个单词的前缀。如果p的失配指针不指向root,则说明序列s[i...m]是某一单词的前缀,于是跳转到p的失配指针,以s[i...m]为前缀继续匹配s[m+1]。
对于已经得到的序列s[1...m],由于s[i...m]可能是某单词的后缀,s[1...j]可能是某单词的前缀,所以s[1...m]中可能会出现单词。此时,p指向已匹配的字符,不能动。于是,令temp = p,然后依次测试s[1...m], s[i...m]是否是单词。
构造的Trie为:
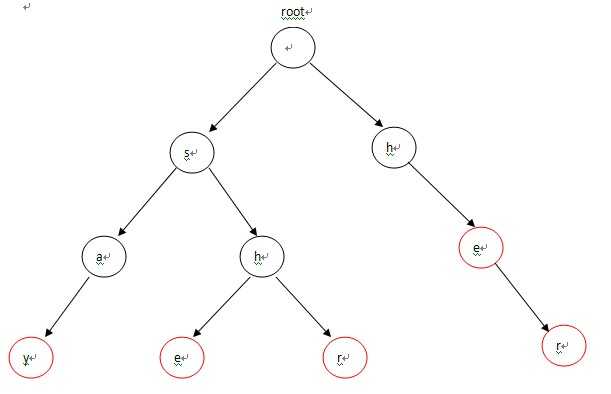
二、构造失败指针
用BFS来构造失败指针,与KMP算法相似的思想。
首先,root入队,第1次循环时处理与root相连的字符,也就是各个单词的第一个字符h和s,因为第一个字符不匹配需要重新匹配,所以第一个字符都指向root(root是Trie入口,没有实际含义)失败指针的指向对应下图中的(1),(2)两条虚线;第2次进入循环后,从队列中先弹出h,接下来p指向h节点的fail指针指向的节点,也就是root;p=p->fail也就是p=NULL说明匹配序列为空,则把节点e的fail指针指向root表示没有匹配序列,对应图-2中的(3),然后节点e进入队列;第3次循环时,弹出的第一个节点a的操作与上一步操作的节点e相同,把a的fail指针指向root,对应图-2中的(4),并入队;第4次进入循环时,弹出节点h(图中左边那个),这时操作略有不同。由于p->next[i]!=NULL(root有h这个儿子节点,图中右边那个),这样便把左边那个h节点的失败指针指向右边那个root的儿子节点h,对应图-2中的(5),然后h入队。以此类推:在循环结束后,所有的失败指针就是下图中的这种形式。
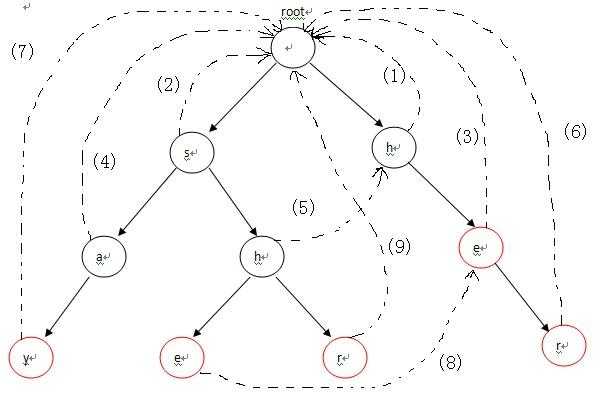
三、扫描
构造好Trie和失败指针后,我们就可以对主串进行扫描了。这个过程和KMP算法很类似,但是也有一定的区别,主要是因为AC自动机处理的是多串模式,需要防止遗漏某个单词,所以引入temp指针。
匹配过程分两种情况:(1)当前字符匹配,表示从当前节点沿着树边有一条路径可以到达目标字符,此时只需沿该路径走向下一个节点继续匹配即可,目标字符串指针移向下个字符继续匹配;(2)当前字符不匹配,则去当前节点失败指针所指向的字符继续匹配,匹配过程随着指针指向root结束。重复这2个过程中的任意一个,直到模式串走到结尾为止。
对照上图,看一下模式匹配这个详细的流程,其中模式串为yasherhs。对于i=0,1。Trie中没有对应的路径,故不做任何操作;i=2,3,4时,指针p走到左下节点e。因为节点e的count信息为1,所以cnt+1,并且讲节点e的count值设置为-1,表示改单词已经出现过了,防止重复计数,最后temp指向e节点的失败指针所指向的节点继续查找,以此类推,最后temp指向root,退出while循环,这个过程中count增加了2。表示找到了2个单词she和he。当i=5时,程序进入第5行,p指向其失败指针的节点,也就是右边那个e节点,随后在第6行指向r节点,r节点的count值为1,从而count+1,循环直到temp指向root为止。最后i=6,7时,找不到任何匹配,匹配过程结束。
三、小试牛刀
代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e7 + 5;
const int MAX = 10000000;
int cnt;
struct node{
node *next[26];
node *fail;
int sum;
};
node *root;
char key[70];
node *q[MAX];
int head,tail;
node *newnode;
char pattern[maxn];
int N;
void Insert(char *s)
{
node *p = root;
for(int i = 0; s[i]; i++)
{
int x = s[i] - ‘a‘;
if(p->next[x] == NULL)
{
newnode=(struct node *)malloc(sizeof(struct node));
for(int j=0;j<26;j++) newnode->next[j] = 0;
newnode->sum = 0;newnode->fail = 0;
p->next[x]=newnode;
}
p = p->next[x];
}
p->sum++;
}
void build_fail_pointer()
{
head = 0;
tail = 1;
q[head] = root;
node *p;
node *temp;
while(head < tail)
{
temp = q[head++];
for(int i = 0; i <= 25; i++)
{
if(temp->next[i])
{
if(temp == root)
{
temp->next[i]->fail = root;
}
else
{
p = temp->fail;
while(p)
{
if(p->next[i])
{
temp->next[i]->fail = p->next[i];
break;
}
p = p->fail;
}
if(p == NULL) temp->next[i]->fail = root;
}
q[tail++] = temp->next[i];
}
}
}
}
void ac_automation(char *ch)
{
node *p = root;
int len = strlen(ch);
for(int i = 0; i < len; i++)
{
int x = ch[i] - ‘a‘;
while(!p->next[x] && p != root) p = p->fail;
p = p->next[x];
if(!p) p = root;
node *temp = p;
while(temp != root)
{
if(temp->sum >= 0)
{
cnt += temp->sum;
temp->sum = -1;
}
else break;
temp = temp->fail;
}
}
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
root=(struct node *)malloc(sizeof(struct node));
for(int j=0;j<26;j++) root->next[j] = 0;
root->fail = 0;
root->sum = 0;
scanf("%d",&N);
getchar();
for(int i = 1; i <= N; i++)
{
gets(key);
Insert(key);
}
gets(pattern);
cnt = 0;
build_fail_pointer();
ac_automation(pattern);
printf("%d\n",cnt);
}
return 0;
}
标签:can 失败 nod 说明 style 理解 malloc 变化 没有
原文地址:http://www.cnblogs.com/xzxl/p/7253103.html