数据结构8——最短路径

标签：floyd   元素   算法   竞赛   最短路   floyd算法   ref   优化   target   

一、最短路径

最短路径：从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径。

1. Dijkstra算法
2. Bellman-Ford算法
3. Floyd算法
4. SPFA算法

二、负权问题

如果一个图仅仅是存在负权，但不构成负权回路，又该如何？

• Dijkstra 算法

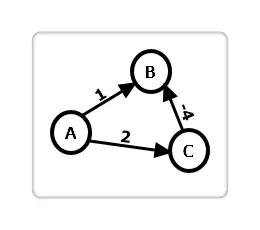
观察上图，若 A 作为源点，在第一轮循环后，B 被标记数组标记，但我们发现在第二轮循环中，B 还可以通过 C 点继续进行更新。由此，可以得出结论：Dijkstra 算法不适用于负权图。

• Bellman_Ford 算法和 SPFA 算法

我们先思考下上述 “因 B 点被标记数组标记而导致无法通过 C 点再更新” 的问题，归根结底是标记数组的锅。有人提议，不妨去掉标记数组，如果去掉，就会造成很严重的问题，首当其冲的是“无法求出dist[]的最小值”。

反观 Bellman_Ford 算法和 SPFA 算法，它们不存在标记数组的问题，因此对于仅仅存在负权的图，它们都可以工作的很好。

最后，读者需要注意的是，如果是无向图，只要存在一条负边，该图就存在负权回路，这不难理解，无向图的一条边相当于有向图的往返两条边。

Dijkstra，Bellman_Ford 和 SPFA，该用哪个？

Bellman_Ford 没什么好说的，能不用就不用。

国际上一般不承认 SPFA 算法，因为在 SPFA 算法论文中对它的复杂度证明存在错误，其次 Bellman_Ford 的论文中已提及过这个队列优化。

SPFA 算法有两个优化策略 SLF 和 LLL。

• SLF，Small Label First 策略，设要加入的节点是 j，队首元素为 i，若dist[j] < dist[i]，则将 j 插入队首，否则插入队尾；
• LLL，Large Label Last 策略，设队首元素为 i，队列中所有 dist 值的平均值为 x，若dist[i] > x则将 i 插入到队尾，查找下一元素，直到找到某一 i 使得dist[i] <= x，则将 i 出队进行松弛操作。

SLF 可使速度提高 15 ~ 20%，SLF + LLL 可提高约 50%。 在实际的应用中 SPFA 的算法时间效率不是很稳定，为了避免最坏情况的出现，通常使用效率更加稳定的 Dijkstra 算法。

使用邻接表 + 二叉堆优化的 Dijkstra 算法，复杂度适宜，也稳定，就是有个缺陷，不能处理负权回路。

最后话个唠，我发现在算法竞赛中我们大多数的选择还是 SPFA，知乎了下，邻接表 + 二叉堆优化的 Dijkstra 写起来复杂，容易错，而 SPFA 代码简单，容易写，但是会被题目卡数据。

总结：首选 Dijkstra，其次 SPFA，最后 Bellman_Ford，具体采用哪种方法，视情况而定。

数据结构8——最短路径

标签：floyd   元素   算法   竞赛   最短路   floyd算法   ref   优化   target   

原文地址：http://www.cnblogs.com/xzxl/p/7277846.html