标签：sig iterator out ++i class names font 技术 sum
题意：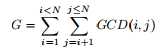
，给定N，求G。
分析：
1、G = f(2) + f(3) + ... + f(n).其中，f(n) = gcd(1, n) + gcd(2, n) + ... + gcd(n - 1, n).
2、设g(n, i)表示gcd(x, n) = i的个数(x < n)，则f(n) = sum{i * g(n, i)}.
3、g(n, i)的求法：
(1)因为gcd(x, n) = i，可得gcd(x / i, n / i) = 1，且x / i < n / i。
(2)因为gcd(x / i, n / i) = 1，所以x / i 与 n / i 互质，即对于n / i来说，比它小且与它互质的数的个数为euler[n / i]，也就是x / i的个数，也就是g(n, i)的个数。
4、所以f(n) = sum{i * euler[n / i]}，枚举质因子即可。
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<cmath>
#include<iostream>
#include<sstream>
#include<iterator>
#include<algorithm>
#include<string>
#include<vector>
#include<set>
#include<map>
#include<stack>
#include<deque>
#include<queue>
#include<list>
#define lowbit(x) (x & (-x))
const double eps = 1e-8;
inline int dcmp(double a, double b){
if(fabs(a - b) < eps) return 0;
return a > b ? 1 : -1;
}
typedef long long LL;
typedef unsigned long long ULL;
const int INT_INF = 0x3f3f3f3f;
const int INT_M_INF = 0x7f7f7f7f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const LL LL_M_INF = 0x7f7f7f7f7f7f7f7f;
const int dr[] = {0, 0, -1, 1, -1, -1, 1, 1};
const int dc[] = {-1, 1, 0, 0, -1, 1, -1, 1};
const int MOD = 1e9 + 7;
const double pi = acos(-1.0);
const int MAXN = 4000001 + 10;
const int MAXT = 250000 + 10;
using namespace std;
int euler[MAXN];
LL ans[MAXN];
void init(){
for(int i = 1; i < MAXN; ++i){
euler[i] = i;
}
for(int i = 2; i < MAXN; ++i){
if(euler[i] == i){
for(int j = i; j < MAXN; j += i){
euler[j] = euler[j] / i * (i - 1);
}
}
}
for(int i = 1; i < MAXN; ++i){
for(int j = i + i; j < MAXN; j += i){
ans[j] += (LL)euler[j / i] * i;
}
}
for(int i = 3; i < MAXN; ++i){
ans[i] += ans[i - 1];
}
}
int main(){
init();
int N;
while(scanf("%d", &N) == 1){
if(N == 0) return 0;
cout << ans[N] << endl;
}
return 0;
}
UVA - 11426 GCD - Extreme (II) （欧拉函数）
标签：sig iterator out ++i class names font 技术 sum
原文地址：http://www.cnblogs.com/tyty-Somnuspoppy/p/7353554.html
