标签:case hdu log 速度 .com 统计 判别式 ilo style
莫比乌斯反演也是反演定理的一种
既然我们已经学了二项式反演定理
那莫比乌斯反演定理与二项式反演定理一样,不求甚解,只求会用
莫比乌斯反演长下面这个样子(=?ω?=)
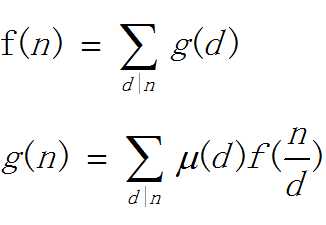
d|n,表示n能够整除d,也就是d是n的所有因子
μ(x)是莫比乌斯函数,它是这样计算的
μ(1) = 1
x = p1 * p2 * p3 ……*pk(x由k个不同的质数组成)则μ(x) = (-1)^k
其他情况,μ (x) = 0
比如
30 = 2 * 3 * 5
μ(30) = (-1)^3
4 = 2 * 2
μ(4) = 0
对于μ(d)函数,它有如下的常见性质:
(1)对任意正整数n有
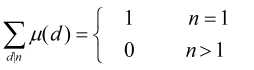
(2)对任意正整数n有
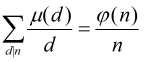
求μ的函数的方法很多
这里提供一种线筛的预处理(复杂度O(n)哟~~~)
#include<cstdio>
const int N = 1e6 + 5;
int mu[N], vis[N], prime[N];
int tot;//用来记录prime的个数
void init(){
mu[1] = 1;
for(int i = 2; i < N; i ++){
if(!vis[i]){
prime[tot ++] = i;
mu[i] = -1;
}
for(int j = 0; j < tot && i * prime[j] < N; j ++){
vis[i * prime[j]] = 1;
if(i % prime[j]) mu[i * prime[j]] = -mu[i];
else{
mu[i * prime[j]] = 0;
break;
}
}
}
}
int main(){
init();
}
上次,有人问我μ为啥不是miu是mu
这。。。当然都可以啦,μ的英文就是mu,miu是读音看你习惯
∑(っ °Д °;)っ为了证明我是对的,我特意百度了希腊字母读音及科学方面应用
|
大写
|
小写
|
英文读音
|
国际音标
|
意义
|
|
Α
|
α
|
alpha
|
/?ælf?/
|
角度,系数,角加速度
|
|
Β
|
β
|
beta
|
/‘beit?/
|
磁通系数,角度,系数
|
|
Γ
|
γ
|
gamma
|
/‘gæm?/
|
电导系数,角度,比热容比
|
|
Δ
|
δ
|
delta
|
/‘delt?/
|
变化量,屈光度,一元二次方程中的判别式
|
|
Ε
|
ε
|
epsilon
|
/ep‘silon/
|
对数之基数,介电常数
|
|
Ζ
|
ζ
|
zeta
|
/‘zi:t?/
|
系数,方位角,阻抗,相对粘度
|
|
Η
|
η
|
eta
|
/‘i:t?/
|
迟滞系数,效率
|
|
Θ
|
θ
|
theta
|
/‘θi:t?/
|
温度,角度
|
|
Ι
|
ι ?
|
iota
|
/ai‘oute/
|
微小,一点
|
|
Κ
|
κ
|
kappa
|
/kæp?/
|
介质常数,绝热指数
|
|
∧
|
λ
|
lambda
|
/‘læmd?/
|
波长,体积,导热系数
|
|
Μ
|
μ
|
mu
|
/mju:/
|
磁导系数,微,动摩擦系(因)数,流体动力粘度
|
|
Ν
|
ν
|
nu
|
/nju:/
|
磁阻系数,流体运动粘度,光子频率
|
|
Ξ
|
ξ
|
xi
|
/ksi/
|
随机数,(小)区间内的一个未知特定值
|
|
Ο
|
ο
|
omicron
|
/oumaik‘r?n/
|
高阶无穷小函数
|
|
∏
|
π
|
pi
|
/pai/
|
圆周率,π(n)表示不大于n的质数个数
|
|
Ρ
|
ρ
|
rho
|
/rou/
|
电阻系数,柱坐标和极坐标中的极径,密度
|
|
∑
|
σ ?
|
sigma
|
/‘sigm?/
|
总和,表面密度,跨导,正应力
|
|
Τ
|
τ
|
tau
|
/tau/
|
时间常数,切应力
|
|
Υ
|
υ
|
upsilon
|
/ju:p‘sil?n/
|
位移
|
|
Φ
|
φ
|
phi
|
/fai/
|
磁通,角,透镜焦度,热流量
|
|
Χ
|
χ
|
chi
|
/kai/
|
统计学中有卡方(χ^2)分布
|
|
Ψ
|
ψ
|
psi
|
/psai/
|
角速,介质电通量
|
|
Ω
|
ω
|
omega
|
/‘oumig?/
|
欧姆,角速度,交流电的电角度
|
其实莫比乌斯有两种描述
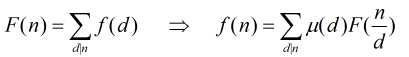
莫比乌斯第一种描述,一般是这种
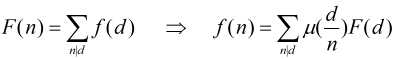
莫比乌斯第二种描述,这种也可以而且有些题这种更好
来做题吧
hdu 1695
http://acm.hdu.edu.cn/showproblem.php?pid=1695
(这题就是容斥那一章的,我就把下面的题意照搬过来了,还记得题目的就跳过题目吧)
题意:给你5个数a,b,c,d,k
在a~b中选一个x, c~d中选一个y,满足gcd(x,y) = k , 求(x,y) 的对数
a, b, c, d, k, 0 < a <= b <= 100,000, 0 < c <= d <= 100,000, 0 <= k <= 100,000
在题目描述的最后一行有一句话,多组里面所有的a和c都是1(这题目不是坑爹吗(╯‵□′)╯︵┻━┻那输入a和c有什么用)
然后题目变成
在1~b中选一个x, 1~d中选一个y,满足gcd(x,y) = k , 求(x,y) 的对数 。。。(无语中。。。)
前面思路一样
先把问题就转化为求1~a区间 和 1~b区间,gcd(x,y) = 1对数的问题
设f(d)为满足gcd(x,y)=d的x,y的对数
我们根据莫比乌斯第二描述来做
那F(1) = f(1) + f(2) + f(3) + ....
F(2) = f(2) + f(4) + f(6) +.....
我们可以看出F(d)就是满足gcd(x,y)为d的倍数的x,y的对数
那F(d)的公式就容易求了
F(d) = (a/d) * (b/d)
(在1~a中,有a/d个数是d的倍数,在1~b中,有b/d个数是d的倍数,这些数不管怎么选择,构成的gcd(x,y)都是d的倍数)
因为
F(1) = f(1) + f(2) + f(3) + ....
所以
f(1) = μ(1)*F(1) + μ(2)*F(2) + μ(3)*F(3) + ...
AC代码:

#include<cstdio> #include<algorithm> using namespace std; typedef long long LL; const int N = 1e6 + 5; int mu[N], vis[N], prime[N]; int tot;//用来记录prime的个数 void init(){ mu[1] = 1; for(int i = 2; i < N; i ++){ if(!vis[i]){ prime[tot ++] = i; mu[i] = -1; } for(int j = 0; j < tot && i * prime[j] < N; j ++){ vis[i * prime[j]] = 1; if(i % prime[j]) mu[i * prime[j]] = -mu[i]; else{ mu[i * prime[j]] = 0; break; } } } } LL Mobius(int a, int b){ LL ret = 0; for(int i = 1; i <= a; i ++){//因为公式中有a/i,所以for到a就可以了 ret += 1ll * mu[i] * (a / i) * (b / i); } //我们现在求完了总对数,但是题目要求的类似(5,7)和(7,5)算一种 //所以接下来我们开始去重 LL temp = 0; for(int i = 1; i <= a; i ++){ temp += 1ll * mu[i] * (a / i) * (a / i); } return ret - temp / 2; //比如a=5,b=7那么(4,6)这样子的区间不可能有重复的(6,4) //所以重复的部分只在1~a中,所以最后减去一半的重复区间就好了 } int main(){ init(); int T, a, b, c, d, k; scanf("%d", &T); for(int cas = 1; cas <= T; cas ++){ scanf("%d%d%d%d%d", &a, &b, &c, &d, &k); if(k == 0){ printf("Case %d: 0\n", cas); continue; } b /= k; d /= k; if(b > d) swap(b, d); printf("Case %d: %I64d\n", cas, Mobius(b, d)); } }
/////////////////此处施工中//////////////////
暂时弃坑。。。。
http://acm.hust.edu.cn/vjudge/contest/view.action?cid=94200#overview
峰神挂的莫比乌斯反演章节,有兴趣自己去做做,不会的去百度。。。。
标签:case hdu log 速度 .com 统计 判别式 ilo style
原文地址:http://www.cnblogs.com/xzxl/p/7354153.html