阿申准备报名参加GT考试,准考证号为N位数X1X2....Xn(0<=Xi<=9),他不希望准考证号上出现不吉利的数字。
他的不吉利数学A1A2...Am(0<=Ai<=9)有M位,不出现是指X1X2...Xn中没有恰好一段等于A1A2...Am. A1和X1可以为
0
标签:turn noi log std div else ring main 等于
阿申准备报名参加GT考试,准考证号为N位数X1X2....Xn(0<=Xi<=9),他不希望准考证号上出现不吉利的数字。
他的不吉利数学A1A2...Am(0<=Ai<=9)有M位,不出现是指X1X2...Xn中没有恰好一段等于A1A2...Am. A1和X1可以为
0
第一行输入N,M,K.接下来一行输入M位的数。 N<=10^9,M<=20,K<=1000
阿申想知道不出现不吉利数字的号码有多少种,输出模K取余的结果.
设a[k][j]为k位后面加一个字母转移到j的方案数,于是:
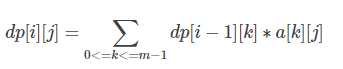
我们发现k后面加一个字母转移到j可以用kmp实现。
这个式子是线性的,可以用矩阵优化。
#include<map> #include<cmath> #include<queue> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define inf 1000000007 #define ll long long #define N 22 #define F(i,r) for(i=0;i<r;i++) struct zz{int q[N][N];}a,b; int n,m,p; zz operator*(zz k,zz l) { int i,j,o;zz z; F(i,m) F(j,m) z.q[i][j]=0; F(i,m) F(j,m) F(o,m) z.q[i][j]=(z.q[i][j]+k.q[i][o]*l.q[o][j])%p; return z; } void ksm(int x) { for(int i=0;i<m;i++) b.q[i][i]=1; while(x) { if(x&1) b=b*a; a=a*a;x>>=1; } } char s[N]; int nxt[N],ans; int main() { scanf("%d%d%d%s",&n,&m,&p,s+1); for(int i=2,j=0;i<=m;i++) { while(j&&s[i]!=s[j+1]) j=nxt[j]; if(s[j+1]==s[i]) j++; nxt[i]=j; } for(int i=0;i<m;i++) { for(int j=0,x;j<10;j++) { x=i; while(x&&s[x+1]-‘0‘!=j) x=nxt[x]; if(j==s[x+1]-‘0‘) a.q[i][x+1]++; else a.q[i][0]++; } } ksm(n); for(int i=0;i<m;i++) ans+=b.q[0][i]; printf("%d\n",ans%p); return 0; }
bzoj 1009: [HNOI2008]GT考试 -- KMP+矩阵
标签:turn noi log std div else ring main 等于
原文地址:http://www.cnblogs.com/lkhll/p/7381750.html