Luogu P1170 兔八哥与猎人

标签：距离   分割线   绝对值   solution   mod   span   题目   logs   pascal   

题目描述

兔八哥躲藏在树林旁边的果园里。果园有M × N棵树，组成一个M行N列的矩阵，水平或垂直相邻的两棵树的距离为1。兔八哥在一棵果树下。

猎人背着猎枪走进了果园，他爬上一棵果树，准备杀死兔八哥。

如果猎人与兔八哥之间没有其它的果树，猎人就可以看到兔八哥。

现己知猎人和兔八哥的位置，编写程序判断兔子所在的位置是否安全.

输入输出格式

输入格式：

第一行为n，表示有n(n ≤ 100,000)组数据，每组数据的第一行为两个正整数ax和ay，表示猎人的位置，第二行为两个正整数bx和by，表示兔八哥的位置(1 ≤ ax, ay, bx, by ≤ 100,000,000)。

输出格式：

共有n行，每行为“yes”或“no”表示兔八哥的位置是否安全。

输入输出样例

1
1 1
1 2

no

Solution

有陷阱！

第一眼看这道题时，估计很多人与我也一样认为只应判断兔八哥周围八个格（如下图A与B,A与C的关系）是否存在猎人，然而事实并非如此！！！（你们想太少了） 

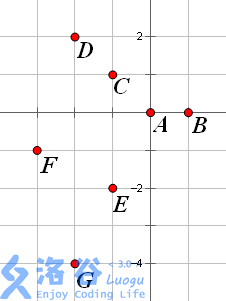
1. 如图，我们可以很直观的看出其实若猎人在E、F，可怜的兔八哥A可谓在劫难逃，所以我们发现猎人的合理站位不局限于兔八哥周围八个格。

2. 如图，我们还能知道若猎人在D、G两点兔八哥是安全的，所以我们便要拿这两个点开刀（并与C、E做对比）。

3. 我们假设兔八哥的坐标是(0,0)，则D为(2,2)，C为(1,1)；G为(-2,-4)，E为(-1,-2)。

4. 我们可以发现兔八哥要想成功躲避猎人，它与猎人横坐标之差的绝对值肯定和它与挡住他（它）们的那棵树横坐标之差的绝对值呈倍数关系，纵坐标亦然（句子有点长，请自行理解）。所以兔八哥要想躲避猎人的攻击，它与猎人横纵坐标之差的绝对值必须同时是一个大于1的整数的倍数，所以它们的最大公约数非1，意思是它们不互质（输出yes）。所以猎人要想杀死兔八哥，自然要将它们互质（输出no）。

5. 完毕！

——————分割不完全的分割线——————

以下是pascal代码：

var n,m,i,j,k,x1,y1,x2,y2:longint;
function go(x,y:longint):longint;//求最大公约数（辗转相除法）
begin
  if y=0 then
  exit(x)
  else
  go:=go(y,x mod y);
end;
begin
  readln(n);//读入数据组数
  for m:=1 to n do
  begin
    readln(x1,y1);//读入猎人的坐标
    readln(x2,y2);//读入兔八哥的坐标
    if go(abs(x1-x2),abs(y1-y2))=1 then//判断是否互质（最大公约数为1）
    writeln(‘no‘)
    else
    writeln(‘yes‘);
  end;
end.

Luogu P1170 兔八哥与猎人

标签：距离   分割线   绝对值   solution   mod   span   题目   logs   pascal   

原文地址：http://www.cnblogs.com/qbwhtc/p/7384826.html