AHOI 2005--洗牌(扩展欧几里得&快速幂)

标签：pac   联想   std   cpp   ges   并且   image   置换   ace   

        发现BZOJ上也是有不少水题的哦！

        排名进前3000也是很容易的哦！

        然后就要继续刷题了哦！

题意

        为了表彰小联为Samuel星球的探险所做出的贡献，小联被邀请参加Samuel星球近距离载人探险活动。

        由于Samuel星球相当遥远，科学家们要在飞船中度过相当长的一段时间，小联提议用扑克牌打发长途旅行中的无聊时间。玩了几局之后，大家觉得单纯玩扑克牌对于像他们这样的高智商人才来说太简单了。有人提出了扑克牌的一种新的玩法。

        对于扑克牌的一次洗牌是这样定义的，将一叠N（N为偶数）张扑克牌平均分成上下两叠，取下面一叠的第一张作为新的一叠的第一张，然后取上面一叠的第一张作为新的一叠的第二张，再取下面一叠的第二张作为新的一叠的第三张……如此交替直到所有的牌取完。

       如果对一叠6张的扑克牌1 2 3 4 5 6，进行一次洗牌的过程如下图所示：

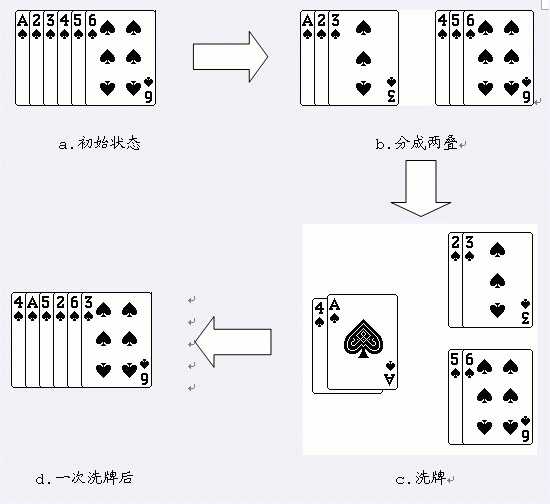
       从图中可以看出经过一次洗牌，序列1 2 3 4 5 6变为4 1 5 2 6 3。当然，再对得到的序列进行一次洗牌，又会变为2 4 6 1 3 5。

       游戏是这样的，如果给定长度为N的一叠扑克牌，并且牌面大小从1开始连续增加到N（不考虑花色），对这样的一叠扑克牌，进行M次洗牌。最先说出经过洗牌后的扑克牌序列中第L张扑克牌的牌面大小是多少的科学家得胜。小联想赢取游戏的胜利，你能帮助他吗？

        输入格式：

               输入文件中有三个用空格间隔的整数，分别表示N，M，L。（其中0＜N≤10^10 ，0 ≤M≤10^10，且N为偶数）。

        输出格式：

               单行输出指定的扑克牌的牌面大小。

Solution

        差点看成置换群的题目。。。结果只是道水题。。。

        容易看出每张牌的位移方式是一样的。。。

        设某张牌在N张牌中初始位置在x，那么一次洗牌后位置就变为(2*x)%(N+1)；

        那样就能得到方程：x*(2^M) Ξ L (mod N+1)

        其中(2^M)可以快速幂取模，于是又得到新方程：x*k Ξ L (mod N+1)；

        典型的扩展欧几里得。。。

代码

#include<cstdio>
#define LL long long
using namespace std;
LL d=0,x=0,y=0;
LL pow(LL a,LL b,LL mod){
    LL s=1;
    while(b){
        if(b&1) s=(s*a)%mod;
        b>>=1;
        a=(a*a)%mod;
    }
    return s;
}
void gcd(LL a,LL b,LL &d,LL &x,LL &y){
    if (b==0){
        d=a;
        x=1;
        y=0;
        return ;
    }
    gcd(b,a%b,d,y,x);
    y-=a/b*x;
    return;
}
int main(){
    LL n,m,l,k;
    scanf("%lld%lld%lld",&n,&m,&l);
    n++;
    k=pow(2,m,n);
    gcd(k,n,d,x,y);
    while(x<0) x+=n;
    d=(l/d)*x%n;
    printf("%lld",d);
    return 0;
}

This passage is made by Yukino.

AHOI 2005--洗牌(扩展欧几里得&快速幂)

标签：pac   联想   std   cpp   ges   并且   image   置换   ace   

原文地址：http://www.cnblogs.com/Yuigahama/p/7392230.html