树链剖分

标签：size   ima   alt   span   结构   知识   image   树状   个数   

树链剖分

定义：

    树链剖分，计算机术语，指一种对树进行划分的算法，它先通过轻重边剖分将树分为多条链，保证每个点属于且只属于一条链，然后再通过数据结构（树状数组、SBT、SPLAY、线段树等）来维护每一条链。

作用：

    可以减少时间复杂度，减少为O(n log n)。

大体思路：

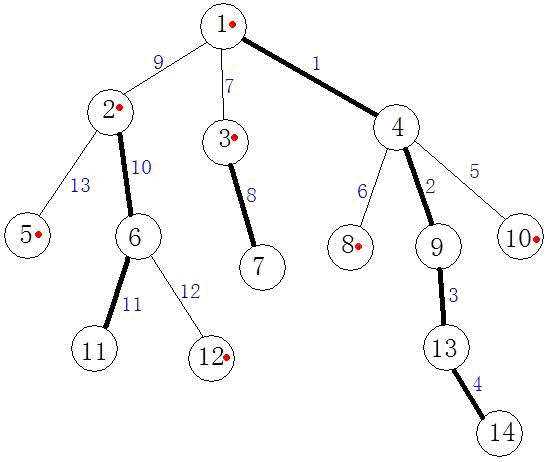
    如图中，加粗体为重边，未加粗的为轻边。在一棵子树中，我们以它的深度（deep）来作为这课子树的大小。我们把一棵树中，链接最大子树的边定为重边，其余的边为轻边，跑一次dfs即可。

    可以用来修改其中某一个节点，或用来询问某一段路径的权值和，或最大值。

时间复杂度的证明：

    当从一条节点数为x的轻边往上搜，遇到一条重边时，重边的节点数至少为x。

    那么当前的子树至少为2x+1。这样一路上去，如果又遇到一条重边，那么至少为2x+1，那么新的子树至少为2*（2x+1）+1。这样一路上去，很快就会达到n。

补充一个小知识点：

    为了避免memset清空较大的复杂度，可以用一种O（1）的办法清空，假设现在是第i次操作，则判断flag（标记）数组是否为i，如果不为i，说明这个数组在这一次还没有用过，那么把这个数组清空为0，否则说明是用过的，可以正常加值。

树链剖分

标签：size   ima   alt   span   结构   知识   image   树状   个数   

原文地址：http://www.cnblogs.com/yiyiyizqy/p/7397846.html