标签:概率分布 不等式 一个 ges href 通过 john 需要 str
1. 相对熵的认识
相对熵又称互熵,交叉熵,鉴别信息,Kullback熵,Kullback-Leible散度(即KL散度)等。设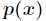 和
和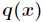
是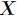 取值的两个概率概率分布,则
取值的两个概率概率分布,则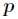 对
对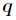 的相对熵为
的相对熵为
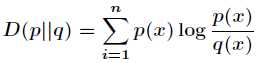
在一定程度上,熵可以度量两个随机变量的距离。KL散度是两个概率分布P和Q差别的非对称性的度量。KL散度是
用来度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。 典型情况下,P表示数据的真实分布,Q
表示数据的理论分布,模型分布,或P的近似分布。
2. 相对熵的性质
相对熵(KL散度)有两个主要的性质。如下
(1)尽管KL散度从直观上是个度量或距离函数,但它并不是一个真正的度量或者距离,因为它不具有对称性,即
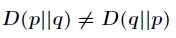
(2)相对熵的值为非负值,即
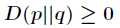
在证明之前,需要认识一个重要的不等式,叫做吉布斯不等式。内容如下

相对熵的应用
相对熵可以衡量两个随机分布之间的距离,当两个随机分布相同时,它们的相对熵为零,当两个随机分布的差别增
大时,它们的相对熵也会增大。所以相对熵(KL散度)可以用于比较文本的相似度,先统计出词的频率,然后计算
KL散度就行了。另外,在多指标系统评估中,指标权重分配是一个重点和难点,通过相对熵可以处理。
在Julia中,有一个KLDivergence包,用来计算两个分布之间的K-L距离,它需要依赖Distributions包,用
法详见:https://github.com/johnmyleswhite/KLDivergence.jl

标签:概率分布 不等式 一个 ges href 通过 john 需要 str
原文地址:http://www.cnblogs.com/smuxiaolei/p/7400908.html