标签:log href return 应用 技术 .com 利用 二次 val
已知n条二次曲线si(x) = ai*x^2 + bi*x + ci(ai ≥ 0),定义F(x) = max{si(x)},求出F(x)在[0,1000]上的最小值.
链接:传送门
分析:最大值最小,我们可以利用二分来解,但是有一个更牛的方法叫:“三分法”,这个方法的应用范围是凸函数,可以看一个图像: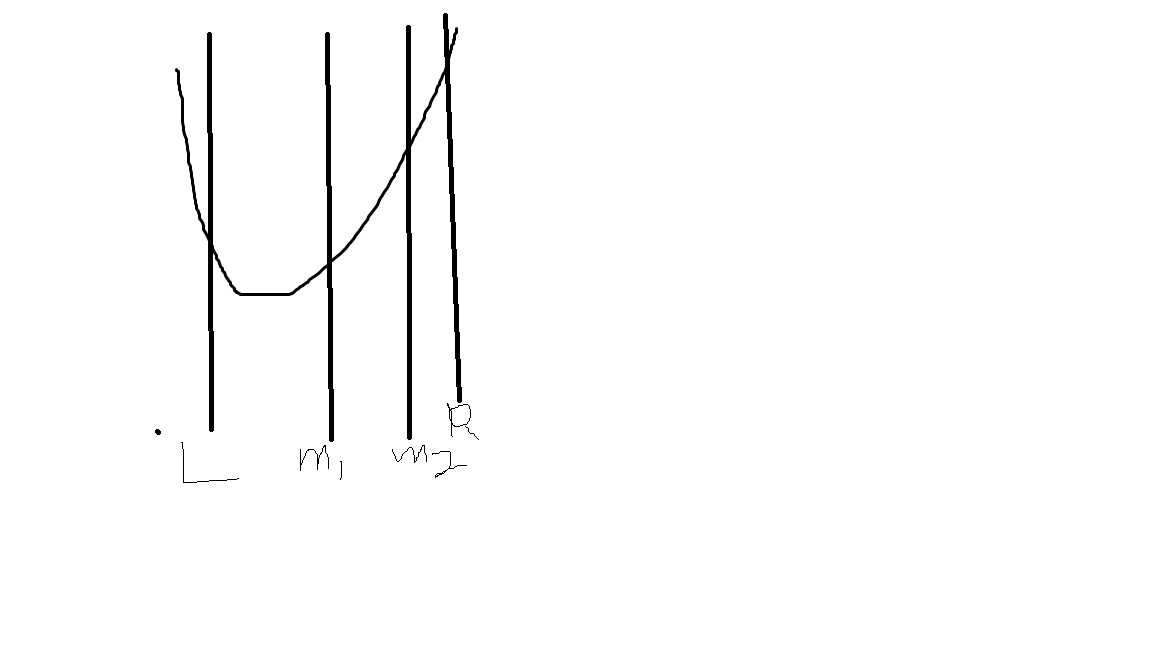
L和R是边界,m1,m2是三等分点,如果f(m1) < f(m2),那么最小值肯定在[l,m2]内,注意,不是[l,m1]因为如果m1在最低点右边,那么就会矛盾,同理,如果f(m2) < f(m1),那么最小值肯定在[m1,r]之间,剩下的操作和二分法基本上就是一样的了。
对于本题而言,可以看出也是一个凸函数,所以我们可以利用三分法来快速求最小值.
#include<iostream> #include<cstdio> #include<cstring> #include<queue> #include<cmath> #include<map> #include<string> using namespace std; const int maxn = 10010; int n, a[maxn], b[maxn], c[maxn],t; double f(double x) { double ans = a[1] * x * x + b[1] * x + c[1]; for (int i = 2; i <= n; i++) ans = max(ans, a[i] * x*x + b[i] * x + c[i]); return ans; } int main() { scanf("%d", &t); while (t--) { scanf("%d", &n); for (int i = 1; i <= n; i++) scanf("%d%d%d", &a[i], &b[i], &c[i]); double L = 0.0, R = 1000.0; while (R - L > 0.000000001) { double m1 = L + (R - L) / 3, m2 = R - (R - L) / 3; if (f(m1) < f(m2)) R = m2; else L = m1; } printf("%.4lf\n", f(L)); } return 0; }
标签:log href return 应用 技术 .com 利用 二次 val
原文地址:http://www.cnblogs.com/zbtrs/p/7413234.html