标签:names 坐标 print alt 三角形 表示 sam 矩形区域 个数
题目描述
输入
输出
为了防止输出数据过大,设f_i表示第i个询问的答案,则你需要输出一行一个整数,即:
样例输入
3 4 5 2 3 7
样例输出
3350931807
题解
前缀和
考虑答案怎么组成:
(0,0)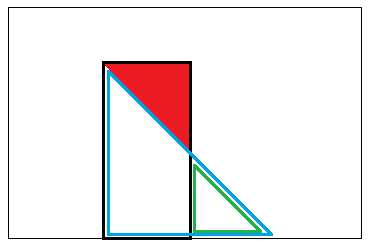
显然答案(红色区域)等于黑色边框(矩形)面积 - 蓝色边框(大三角形)面积 + 绿色边框(小三角形)面积。
于是维护两种前缀和:第一种维护一般的矩形区域二维前缀和,第二种维护直角边边长为x,左下角横坐标为y,纵坐标为1的等腰直角三角形的数之和。
然后乱搞就过了。为了防止n和m弄混,可以令n‘=m‘=max(n,m)。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define N 3010
using namespace std;
unsigned A , B , C , a[N][N] , sum[N][N] , ste[N][N];
inline unsigned rng61()
{
A ^= A << 16;
A ^= A >> 5;
A ^= A << 1;
unsigned t = A;
A = B;
B = C;
C ^= t ^ A;
return C;
}
int main()
{
int n , m , q , i , j , x , y , k;
unsigned ret , ans = 0;
scanf("%d%d%d%u%u%u" , &n , &m , &q , &A , &B , &C);
for(i = 1 ; i <= n ; i ++ )
for(j = 1 ; j <= m ; j ++ )
a[i][j] = rng61();
for(i = 1 ; i <= max(n , m) ; i ++ )
for(j = 1 ; j <= max(n , m) ; j ++ )
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + a[i][j];
for(i = 1 ; i <= max(n , m) ; i ++ )
for(j = max(n , m) ; j >= 1 ; j -- )
ste[i][j] = ste[i - 1][j + 1] + sum[j][i] - sum[j - 1][i];
while(q -- )
{
x = rng61() % n + 1;
y = rng61() % m + 1;
k = rng61() % min(x , y) + 1;
ret = (sum[x][y] - sum[x - k][y]) - (ste[y - 1][x - k + 1] - ste[y > k ? y - k - 1 : 0][x + 1]);
ans = ans * 233 + ret;
}
printf("%u\n" , ans);
return 0;
}
标签:names 坐标 print alt 三角形 表示 sam 矩形区域 个数
原文地址:http://www.cnblogs.com/GXZlegend/p/7413438.html