标签:边界值 方法 sub 编号 height 正整数 long 个数 左右
转自:(http://www.cnblogs.com/geek-007/p/7197439.html)
经典例题:加分二叉树(Luogu 1040)
设一个 n 个节点的二叉树 tree 的中序遍历为( 1,2,3,…,n),其中数字 1,2,3,…,n 为节点编号。每个节点都有一个分数(均为正整数),记第 i 个节点的分数为 di, tree 及它的每个子树都有一个加分,任一棵子树 subtree(也包含 tree 本身)的加分计算方法如下:
subtree 的左子树的加分 × subtree 的右子树的加分+ subtree 的根的分数。
若某个子树为空,规定其加分为 1,叶子的加分就是叶节点本身的分数,不考虑它的空子树。
试求一棵符合中序遍历为( 1,2,3,…,n)且加分最高的二叉树 tree。要求输出;
1.tree 的最高加分:
2.tree 的前序遍历:
- 5 7 1 2 10
- 答案 1: 145
- 答案 2: 3 1 2 4 5
设 F[i][j] 为只用第 i 个数到第 j 个数构成的加分树的最大权值。下图为样例解释: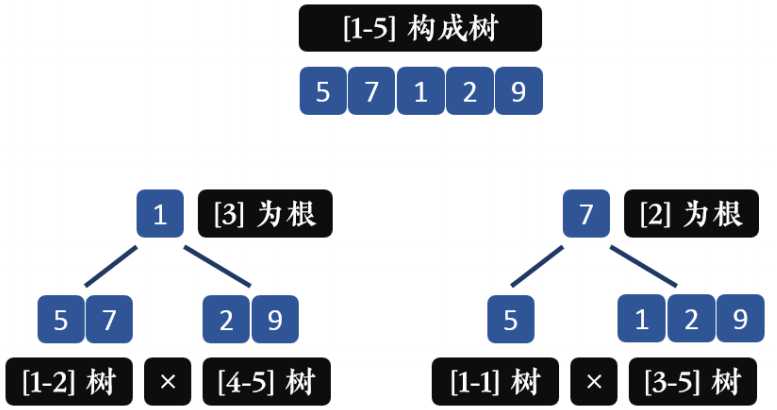
牢记一个二叉树的性质:中序遍历时候,左右子树一定在根节点左右两边
* 枚举根节点,这样就化成了左子树和右子树的问题,求最优解即可。
* F[i][j] = MAX ( F[i][k-1] * F[k+1][j] + A[k] )(左×右+根k自己本身权值)
//T25:加分二叉树 for(int i=1;i<=n;++i) f[i][i]=a[i];//赋初值(只有一个叶子节点,根就是自己) for(int i=0;i<=n;++i) f[i+1][i]=1; for(int k=1;k<n;++k) for(int i=1;i+k<=n;++i) { int j=i+k; for(int l=i;l<=j;++l) f[i][j]=max(f[i][j],f[i][l-1]*f[l+1][j]+a[l]);//枚举根节点 } int ans=f[1][n];
* 问题: 如何求出树的前序遍历(树的形态)?
我们另外记录一个辅助数组 G[i][j],代表 F[i][j] 取最大值的时候,根节点是什么,这样就可以通过递归来求出树的前序遍历。
for(int i=1;i<=n;++i) f[i][i]=a[i],g[i][i]=i;//边界值(只有一个叶子节点,根就是自己) for(int i=0;i<=n;++i) f[i+1][i]=1;//预处理空节点,保证不出错,一个根节点没有左子树,把左子树标记为1 for(int k=1;k<n;++k)//k:区间长度 for(int i=1;i+k<=n;++i) { int j=i+k;//j:末尾节点 for(int l=i;l<=j;++l) { long long t=f[i][l-1]*f[l+1][j]+a[l]; if(t>f[i][j])//记录最优的根 { f[i][j]=t; g[i][j]=l; } } }
//T25:加分二叉树 //递归输出x到y这个树的前缀遍历 void dfs(int x,int y) { if(x>y) return; int l=g[x][y];//l为根 cout<<l<<" ";//先输出l /*=====================*///再输出子树的值 dfs(x,l-1);//左 dfs(l+1,y);//右 /*=====================*/ } ... //输出答案——整棵树 dfs(1,n);
标签:边界值 方法 sub 编号 height 正整数 long 个数 左右
原文地址:http://www.cnblogs.com/oi-forever/p/7416391.html