最大似然与逻辑回归

标签：设置   height   相互   最小化   简单   思想   条件   描述   方向   

1、最大似然

多数情况下我们是根据已知条件来推算结果，而最大似然估计是已经知道了结果，然后寻求使该结果出现的可能性最大的条件，以此作为估计值

求最大似然函数估计值的步骤：

1. 写出似然函数
2. 对似然函数取对数，并整理
3. 求导数，令导数为0，得到似然方程
4. 解似然方程，得到的参数即为所求

2、机器学习算法的学习过程

1. 对于一个问题，用数学语言来描述它，然后建立一个回归/分类模型等来描述这个问题
2. 通过最大似然、最大后验概率或最小化分类误差等建立模型的代价函数，也就是一个最优化问题，找到最优化问题的解，也就是能拟合我们的数据的最好的模型参数
3. 然后我们需要求解这个代价函数，找到最优解，求解时可能存在如下情况：

• 这个优化函数存在解析解。例如我们求最值一般是对代价函数求导，导数为0的点一般就是最值，如果代价函数能简单求导，并且求导后为0的式子存在解析解，那就可以直接得到最优的参数
• 如果式子很难求导，例如函数里面存在隐含的变量或者变量相互间存在耦合，也就互相依赖的情况，或者求导后式子得不到解释解，例如未知参数的个数大于已知方程组的个数等，这时候我们就需要借助迭代算法来找到最优解
• 如果代价函数是凸函数，那么就存在全局最优解，但如果是非凸的，那么就会有很多局部最优的解

3、逻辑回归

Logistic regression可以用来回归，也可以用来分类（主要是二分类），就是面对一个回归/分类问题，建立代价函数，然后通过优化方法迭代求解出最优的模型参数，然后测试这个求解的模型的好坏

假设我们的样本是{x, y}，y是0或者1，表示正类或者负类，x是我们的m维的样本特征向量。那么这个样本x属于正类，也就是y=1的“概率”是：

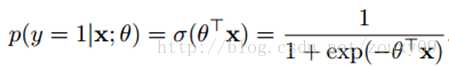
这里θ是模型参数，也就是回归系数，σ是sigmoid函数。实际上这个函数是由下面的对数几率（也就是x属于正类的可能性和负类的可能性的比值的对数）变换得到的：

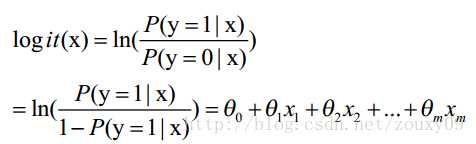
logistic回归就是一个线性分类模型，它与线性回归的不同点在于：它将线性回归输出的很大范围的数，例如从负无穷到正无穷，压缩到0和1之间

LogisticRegression最基本的学习算法是最大似然，按照最大似然函数估计值的一般步骤，先写出似然函数，假设我们有n个独立的训练样本{(x₁, y₁) ,(x₂, y₂),…, (x_n, y_n)}，y={0, 1}。那每一个观察到的样本(x_i, y_i)出现的概率是：

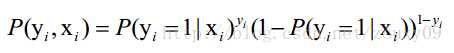
n个独立的样本出现的似然函数为（因为每个样本都是独立的，所以n个样本出现的概率就是他们各自出现的概率相乘）：

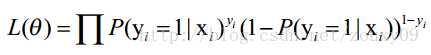
接着变换L,取自然对数，并化简：

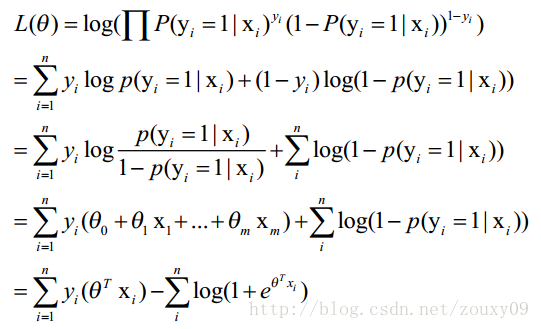
求导：

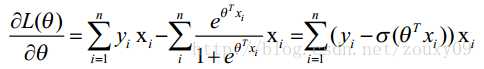
 然后我们令该导数为0，你会很失望的发现，它无法解析求解，只能借助迭代来搞定，这里选用了经典的梯度下降算法

4、梯度下降

Gradient descent 又叫 steepest descent，是利用一阶的梯度信息找到函数局部最优解的一种方法，它的思想是若要找最小值，只需每一步都往下走（也就是每一步都可以让代价函数小一点），然后不断的走，就肯定能走到最小值的地方

但同时也需要更快的到达最小值，所以我们需要每一步都找下坡最快的地方，也就是每一步我走某个方向，都比走其他方法，要离最小值更近。而这个下坡最快的方向，就是梯度的负方向了

对logistic Regression来说，梯度下降算法如下：

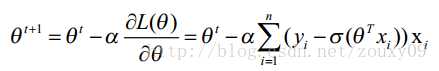
其中，参数α 叫学习率，就是每一步走多远，α如果设置的太多，那么很容易就在最优值附加徘徊，因为你步伐太大了。但如果设置的太小，那收敛速度就太慢了，虽然会落在最优的点，但速度会特别慢

5、一句话解释

Logistic Regression就是一个被logistic方程归一化后的线性回归

参考

http://blog.csdn.net/zouxy09/article/details/8537620

http://blog.csdn.net/zouxy09/article/details/20319673

最大似然与逻辑回归

标签：设置   height   相互   最小化   简单   思想   条件   描述   方向   

原文地址：http://www.cnblogs.com/xiaoyun94/p/7418747.html