标签:总结 逆矩阵 需要 高斯分布 log bsp ack 常用 适合
多元高斯(正态)分布
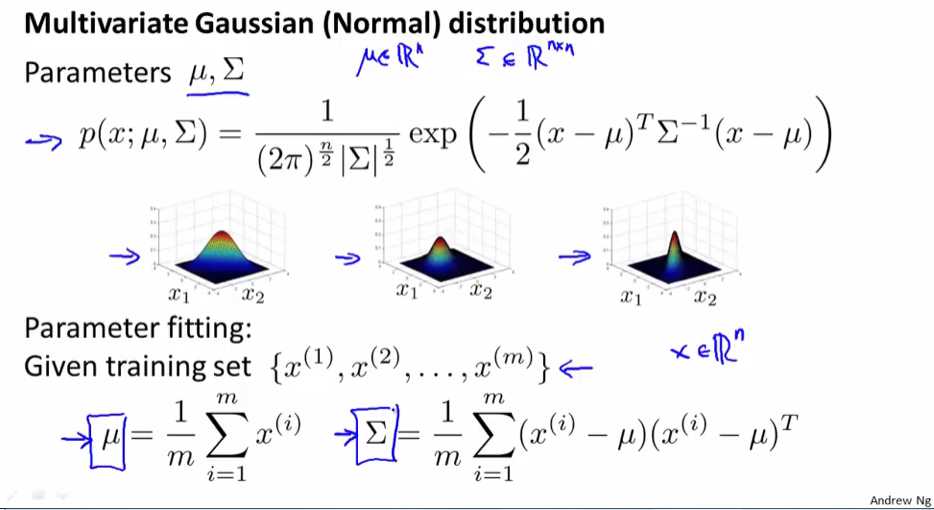
多元高斯分布有两个参数u和Σ,u是一个n维向量,Σ协方差矩阵是一个n*n维矩阵。改变u与Σ的值可以得到不同的高斯分布。
参数估计(参数拟合),估计u和Σ的公式如上图所示,u为平均值,Σ为协方差矩阵
使用多元高斯分布来进行异常检测

首先用我我们的训练集来拟合参数u和Σ,从而拟合模型p(x)
拿到一个新的样本,使用p(x)的计算公式计算出p(x)的值,如果p(x)<ε就将它标记为一个异常点
当我们对上图中那个绿色的点进行异常检测时,这些红色的点服从多元高斯正态分布(x1与x2正相关),算法会将绿色的判断为异常点,因为它远离这个高斯分布中心点。
多元高斯分布模型与原来的模型之间的关系(原来的模型是多元高斯分布的一个特例)
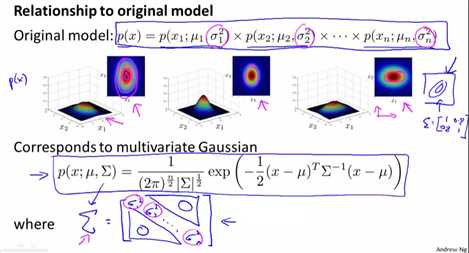
原来的模型p(x)=p(x1)*p(x2)*p(x3).....*p(xn)这个模型那就什么样的多元高斯分布呢?
上面图中三个多元高斯分布的图型,它们的等高线位于x1或者x2轴向线平行,原来的模型即那就于这样的高斯分布,即没有x1,x2的关系约束,即Σ在非对角线上的值为0,只在对角线上有值。
所以原来的模型p(x)对应于下面的多元高斯分布,这个多元高斯分布有个约束条件,即Σ只在对角线上有值(分别为σ12,σ22.....σn2),在非对角线上的值都为0,不能给不同特征之间的相关性建模。
该用哪个模型?

original model可能使用得更频繁,多元高斯模型没有那么常用,但是它能捕捉到不同特征之间的相关性(正相关或者负相关)
在original model里面,如果你想捕获不同特征组合之间的异常(如捕获CPU load与memory use之间组合的不正常情况),我们需要建立一个新的feature=这两个特征之间的组合,如x3=CPU load/memory use.这样虽然当x1是正常的,x2是正常的,但是如果x1/x2不正常,我们就可以捕获到这种异常情况。而多元高斯模型可以自动地捕获不同特征变量之间的相关性。
original model计算比较快,运算量更小,适用于特征量非常多的情况,即n值很大的情况;而当n很大时,多元高斯模型要计算Σ的逆矩阵(为n*n),这个计算量非常大,所以多元高斯模型不适合于n值很大的情况。
对于original model即使m很小,即训练集很小,也可以运行的也可以的;而对于多元高斯模型,在数学上必须满足m>n,不然Σ就是不可逆的,但是在实际中,我们使用时只有m远大于n时,即m>=10n(合理的经验法则)时才使用多元高斯模型。因为Σ是一个n*n的矩阵,有n*n/2个参数(Σ为对称矩阵)需要计算,如果我们的训练样本不够大的话,就不能很好的评估这些参数。
实际中,original model更常用,如果我们想捕捉变量之间的相关性的话就另外创建一个新的feature来捕捉特定的不正常值的组合。
在训练集很大,n不大的情况下,多元高斯模型可以考虑,可以帮你省去创建新的feature的时间。
当拟合多元高斯模型时,如果发现Σ不可逆时(奇异的),会有两种情况导致,一种情况是它没有满足m>n的条件,第二种情况是有冗余的特征变量(如x1=x2,x3=x4+x5(x3是冗余的,没有提供额外的信息)),即线性相关的特征变量。所以当在实际中遇到Σ不可逆时,检查m是否比n大得多,然后检查是否有冗余的特征变量(如删掉x1,x3),这样就能很好地运行了,但是我们遇到这些问题的可能性会比较低,我们可以直接应用多元高斯模型,不需要担心Σ不可逆的问题。
总结
1>使用多元高斯模型可以使我们的算法自动捕获不同特征变量之间的相关性(正相关或者负相关),在组合不正常时将其标识为异常。
标签:总结 逆矩阵 需要 高斯分布 log bsp ack 常用 适合
原文地址:http://www.cnblogs.com/yan2015/p/7419972.html