标签：blog 在线 fine namespace 数学题 int http 在线学习 质因数
数学题第二弹！
求一个给定的圆(x^2+y^2=r^2)，在圆周上有多少个点的坐标是整数。
一个正整数r。
整点个数。
4
4
r<=2000 000 000
小C不想写题解啊啊啊啊！！！！
题解在这里啊啊啊啊！！！！（看完记得投币！！！！）
我爱数学啊啊啊啊！！！！
开玩笑的，还是说一说题解吧。
相信如果你认真看完了上面那个视频的前25min，心里肯定已经有不下一万种解法了。
小C先口胡两句，你们意会就好。
题目要我们求的是以原点为圆心，半径为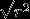
的圆经过了多少个整点。
所以我们只要把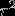
的所有因数的
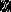函数值相加的和乘上4就是答案。
请完全无视上面两行！完全无视！现在说正经的：
根据我们的知识储备，我们知道，对于圆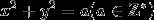
。
将a进行质因数分解，得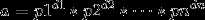
。
如果存在i使得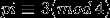
且
为奇数，那么该圆不经过任何整点。
否则答案就是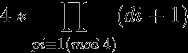
。
根据上面的结论，由于题目中的a是完全平方数，所以不存在di为奇数的情况，因此必定经过整点。
所以我们只要把r质因数分解，挑出其中形如4k+1的质数，该质数的指数为d，对答案的贡献就是乘上2*d+1。
时间复杂度是质因数分解的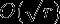
。
#include <cstdio> #include <algorithm> #include <cstring> #define MN 60005 using namespace std; int n,ans,pin,pri[MN]; bool u[MN]; inline int read() { int n=0,f=1; char c=getchar(); while (c<‘0‘ || c>‘9‘) {if(c==‘-‘)f=-1; c=getchar();} while (c>=‘0‘ && c<=‘9‘) {n=n*10+c-‘0‘; c=getchar();} return n*f; } int main() { register int i,j,lt; n=read(); ans=1; for (i=2;1LL*i*i<=n;++i) { if (!u[i]) pri[++pin]=i; for (j=1;1LL*i*i*pri[j]*pri[j]<=n;++j) { u[i*pri[j]]=true; if (i%pri[j]==0) break; } } while (n%pri[1]==0) n/=pri[1]; for (i=2;i<=pin;++i) { for (lt=0;n%pri[i]==0;++lt) n/=pri[i]; if (pri[i]%4==1) ans*=lt<<1|1; } if (n!=1&&n%4==1) ans*=3; printf("%d",ans<<2); }
我在B站学数学.jpg
开什么玩笑！B站本来就是优秀的在线学习网站！（小C口胡不下去了）
标签：blog 在线 fine namespace 数学题 int http 在线学习 质因数
原文地址：http://www.cnblogs.com/ACMLCZH/p/7420813.html
