标签:需要 解决 常见 ble 一个 区间 直线 不等式 方法
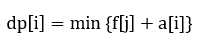
如果a[i]单调增的话,显然可以用减单调队列直接存f[j]进行优化。
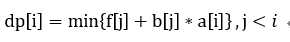
即实现转移方程中的i,j分离。b单调减,a单调增(可选)。
令:
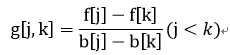
在队首,如果g[j,k]>=-a[i],那么j优于k,而且以后j也优于k,因此k可以重队列中直接删去。在队尾,如果x<y<z,且g[x,y]<=g[y,z],也就是说只要y优于x一定可以得出z优于y的,我们就删去y。
经过队尾的筛选,我们在队列中得到的是一个斜率递减的下凸包,每次寻找从上往下被-a[i]斜率的线所扫到的第一个点,a[i]单调的话通过队首的维护我们可以在均摊O(1)的时间内找到这个点。值得注意的是,即使a[i]不单调,我们仍然可以通过二分在O(log n)的时间内找到转移点。
高维的场合和低维并没有区别。只要使用斜率和单调队列优化,一定可以降一维。高维时可以没有j<i的限制,这时我们理解成若干条b[j]*x+f[j]的直线形成一个下凸包求值器,然后带入一个a[i]作为x计算得的结果就是答案,时间是O(nlogn)。
这是一种很奇怪的情况。有些时候,问题可以转化成给定一堆直线K[i]*X+B[i],每次询问选择连续的一段[a..b]和一个x,求最小值。
做法是构造一个下凸包求值器,实现对给定x求值和合并两个功能,内部实现是按K排好序的线段序列。然后线段树每个节点维护一个求值器。这样可以在O(nlognlogn)的时间内解决问题。
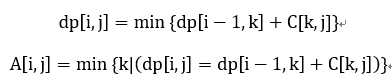
元素的分组合并问题通常拥有以上的形式。优化的条件是A[i,j]的单调性,也就是说A[i,j]<=A[i,j+1]。也即要求C[k,j]满足四边形不等式C[a,c]+C[b,d]<=C[a,d]+C[b,c] 。(含义是:越晚并入新元素,并入的组尺寸越小,其额外代价越小。这里四边形不等式已经是充分条件了,不需要区间单调)
优化的伪代码如下:
compute(i,l,r,ol,or)
1. 令m=(l+r)>>1
2. 寻找k=ol..or,使得dp[i,m]=dp[i-1,k]+C[k,m]最小
3. 如果l==r,返回。否则执行compute(i,l,m-1,ol,k);compute(i,m+1,r,k,or);
四边形不等式优化应用于区间DP:
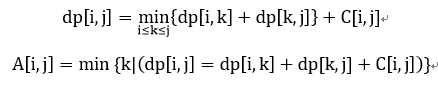
要求C[i,j]满足四边形不等式C[a,c]+C[b,d]<=C[a,d]+C[b,c]和区间单调性C[b,c]<=C[a,d]。注意这里的C不在转移方程的内部,而是一个定值。
满足上件的前提下,有A[i,j-1]<=A[i,j]<=A[i+1,j](关键条件),因此可以优化。优化方法为以|i-j|的递增顺序DP,同时记录各个A[i,j]值,枚举时在A[i,j-1]和A[i+1,j]的区间卡内枚举。
一眼能看出来就是快速幂。多为期望或概率DP。
通常是有不确定的强制转移的场合。如FAFU1231。
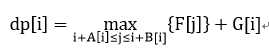
此时因A[i],B[i]欠缺单调性,单调队列的使用受到限制,用线段树即可解决。如斜率优化中掺杂此种限制,则同上3.
标签:需要 解决 常见 ble 一个 区间 直线 不等式 方法
原文地址:http://www.cnblogs.com/Renyi-Fan/p/7421112.html