标签:存在 img 最短路径 树链剖分 养成 ext2 code 需要 for
题意:
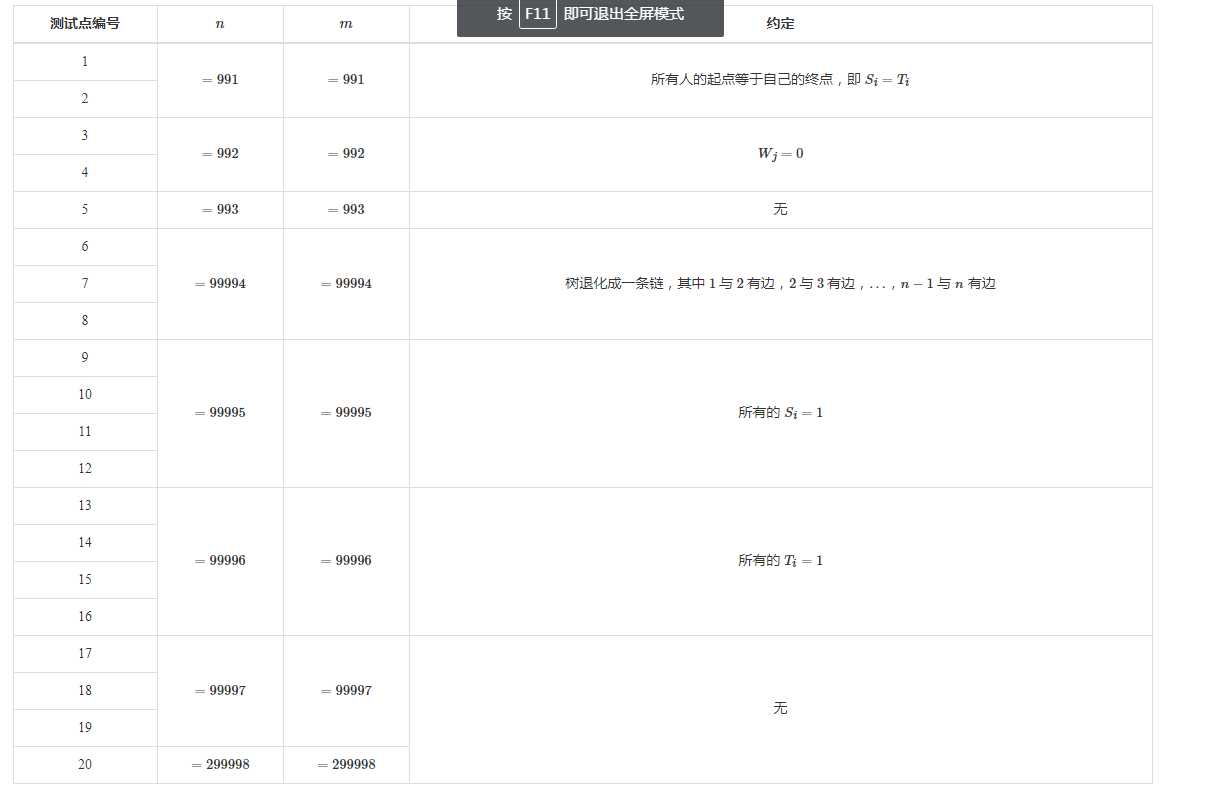
思路:From http://blog.csdn.net/doyouseeman/article/details/53385565
我们思考一下从x到y的路径,
这个可以拆成从x到lca的路径和从lca到y的路径,这个很明显。
如果一个点i在从x到lca 的路径可以检测到的话,
那么就有deep[i]+w[i]=deep[x]。
如果一个点i在从lca到y的路径上可以检测到的话,
那么就有deep[i]-w[i]=deep[y]-t(t表示x到y的路径长度)。
那么用树链剖分的方法很容易,但是很慢。有一个用桶的方法,跑得很快。
维护两个桶,一个向上的桶a和一个向下的桶b。
从x到y的一个路径,在x中a[deep[x]]加一个,当dfs把lca退栈的时候,x的影响就没有了,那么把a[deep[x]]减掉。
在lca那里需要把一个b[deep[y]]加进来,在y出栈后,就把b[deep[y]]减掉。
每次ans[x]的答案就是子树a[deep[x]+w[x]]+b[deep[x]-w[x]]的数量。
但是如果是一条链的情况,那么这样会算重,所以还要减去重复的数量。
1 var shang,xia:array[-310000..310000]of longint; 2 head,head1,head2,head3:array[1..6100000]of longint; 3 vet,vet1,vet2,vet3, 4 next,next1,next2,next3,ans,dep,a,s:array[1..610000]of longint; 5 f:array[1..310000,0..20]of longint; 6 n,m,i,x,y,q,b,tot,tot1,tot2,tot3,t:longint; 7 8 procedure add(a,b:longint); 9 begin 10 inc(tot); 11 next[tot]:=head[a]; 12 vet[tot]:=b; 13 head[a]:=tot; 14 end; 15 16 procedure add1(a,b:longint); 17 begin 18 inc(tot1); 19 next1[tot1]:=head1[a]; 20 vet1[tot1]:=b; 21 head1[a]:=tot1; 22 end; 23 24 procedure add2(a,b:longint); 25 begin 26 inc(tot2); 27 next2[tot2]:=head2[a]; 28 vet2[tot2]:=b; 29 head2[a]:=tot2; 30 end; 31 32 procedure add3(a,b:longint); 33 begin 34 inc(tot3); 35 next3[tot3]:=head3[a]; 36 vet3[tot3]:=b; 37 head3[a]:=tot3; 38 end; 39 40 procedure dfs(u,fa:longint); 41 var e,v,i:longint; 42 begin 43 for i:=1 to 20 do 44 begin 45 if dep[u]<(1<<i) then break; 46 f[u,i]:=f[f[u,i-1],i-1]; 47 end; 48 e:=head[u]; 49 while e<>0 do 50 begin 51 v:=vet[e]; 52 if v<>fa then 53 begin 54 f[v,0]:=u; 55 dep[v]:=dep[u]+1; 56 dfs(v,u); 57 end; 58 e:=next[e]; 59 end; 60 end; 61 62 procedure swap(var x,y:longint); 63 var t:longint; 64 begin 65 t:=x; x:=y; y:=t; 66 end; 67 68 function lca(x,y:longint):longint; 69 var i,d:longint; 70 begin 71 if dep[x]<dep[y] then swap(x,y); 72 d:=dep[x]-dep[y]; 73 for i:=0 to 20 do 74 if d and (1<<i)>0 then x:=f[x,i]; 75 for i:=20 downto 0 do 76 if f[x,i]<>f[y,i] then 77 begin 78 x:=f[x,i]; y:=f[y,i]; 79 end; 80 if x=y then exit(x); 81 exit(f[x,0]); 82 end; 83 84 procedure dfs1(u,fa:longint); 85 var e,v,x,y:longint; 86 begin 87 x:=xia[dep[u]+a[u]]; 88 y:=shang[dep[u]-a[u]]; 89 xia[dep[u]]:=xia[dep[u]]+s[u]; 90 e:=head1[u]; 91 while e<>0 do 92 begin 93 v:=vet1[e]; 94 inc(shang[v]); 95 e:=next1[e]; 96 end; 97 e:=head[u]; 98 while e<>0 do 99 begin 100 v:=vet[e]; 101 if v<>fa then dfs1(v,u); 102 e:=next[e]; 103 end; 104 ans[u]:=xia[dep[u]+a[u]]+shang[dep[u]-a[u]]-x-y; 105 e:=head2[u]; 106 while e<>0 do 107 begin 108 v:=vet2[e]; 109 dec(xia[v]); 110 if v=dep[u]+a[u] then dec(ans[u]); 111 e:=next2[e]; 112 end; 113 e:=head3[u]; 114 while e<>0 do 115 begin 116 v:=vet3[e]; 117 dec(shang[v]); 118 e:=next3[e]; 119 end; 120 end; 121 122 begin 123 assign(input,‘bzoj4719.in‘); reset(input); 124 assign(output,‘bzoj4719.out‘); rewrite(output); 125 readln(n,m); 126 for i:=1 to n-1 do 127 begin 128 readln(x,y); 129 add(x,y); add(y,x); 130 end; 131 dfs(1,0); 132 for i:=1 to n do read(a[i]); 133 for i:=1 to m do 134 begin 135 readln(x,y); 136 q:=lca(x,y); 137 t:=dep[x]+dep[y]-2*dep[q]; 138 inc(s[x]); b:=dep[y]-t; 139 add1(y,b); 140 add2(q,dep[x]); 141 add3(q,b); 142 end; 143 dfs1(1,0); 144 for i:=1 to n-1 do write(ans[i],‘ ‘); 145 write(ans[n]); 146 close(input); 147 close(output); 148 end.
标签:存在 img 最短路径 树链剖分 养成 ext2 code 需要 for
原文地址:http://www.cnblogs.com/myx12345/p/7425300.html