标签:十进制 0.11 16进制 有一个 结束 小数 精确 strong padding
下方灵魂画手出现!!!
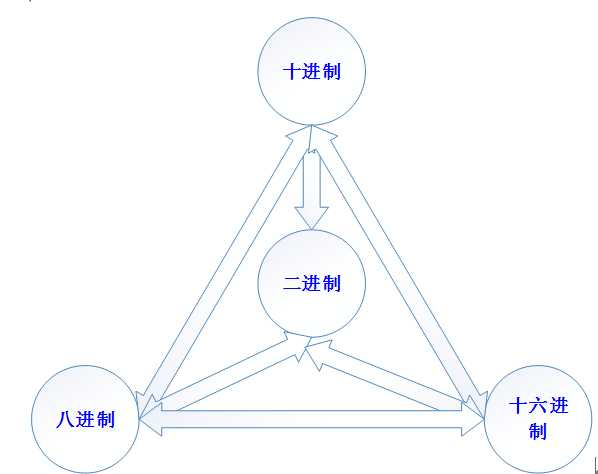
十进制:逢十进一,借一当十!有十个数值位,0-9
二进制:逢二进一,借一当二!有两个数值位,0和1
计算机中,常见的还有8进制和16进制!
其中,
2进制的数值是0和1
10进制数值是0-9
8进制的数值位为0-7
16进制的数值位为0-F,从10开始用字母代替,10:A,15:F
为了使各自进制之间可以互相的转换,引入了权的概念:
(1234.56)10 = 1*103 + 2*102 + 3*101 + 4*100 + 5*10-1 + 6*10-2
上面所有标红的,都叫做十进制的权!
其他各自进制转换为十进制,都是按权展开:
比如:
(1101.11)2 = 1*23 + 1*22 + 0*21 + 1*20 + 1*2-1 + 1*2-2 = (13.75)10
(1234.56)8 = 1*83 + 2*82 + 3*81 + 4*80 + 5*8-1 + 6*8-2
(1234.56)16 = 1*163 + 2*162 + 3*161 + 4*160 + 5*16-1 + 6*16-2
整数部分转换为二进制:
1, 除二取余法:不停的除以2,不停的取余数,一直到商为0为止,然后从下往上依次取得余数即可!
2, 填充法(填“1”法)
拿67为例:
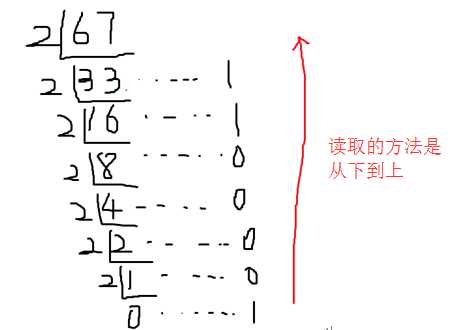
所以,(67)10 = (1000011)2
注:(67)10 = (1000011)2 的意思是67是10进制数值,它的二进制数值是1000011
(13)10= 1*23 + 1*22 + 0*21 + 1*20 =(1101)2
例子1:(67的二进制)
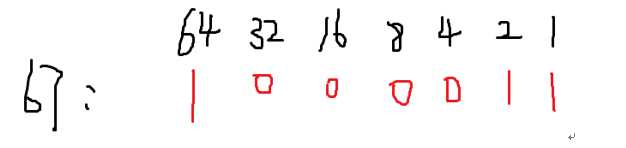
例子2:(769的二进制)

乘二取整法!
不停的拿小数乘于2,不停的取走它的整数部分(注意是取走整数留0),如果取成了0.0就可以结束了,然后是从上往下依次取得整数部分即可!
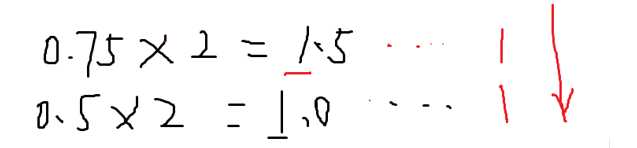
(0.75)10 = (0.11)2
注意:不是每一个小数都可以百分百精确的转换为二进制,我们一般精确到后小数点后5位!
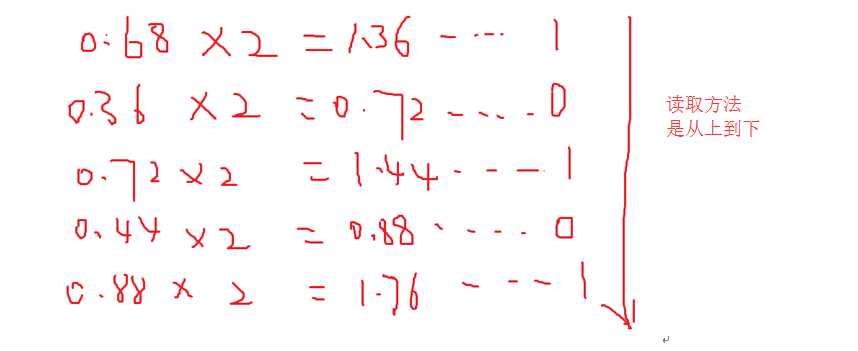
该小数是:0.10101
八与十六进制转换为十进制都是按权展开!
十进制转换为八进制与十六也是整数部分与小数部分分开转换:
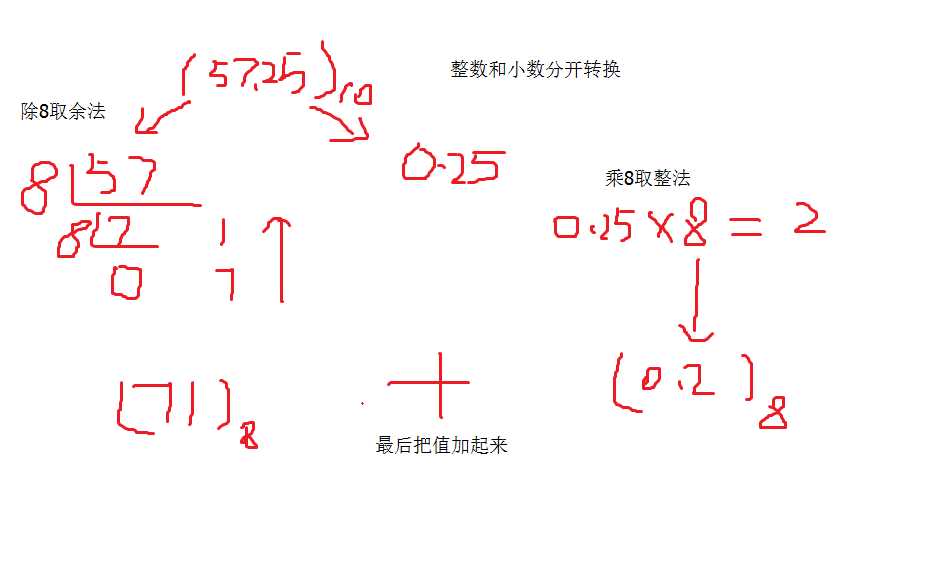
最后(57.25)10 = (71.2)8

(57.25)10 = (39.4)16
注意:
上面的所有的除X取余和乘X取整都只适合十进制与其他进制之间的互转!
有一个方法就是以十进制作为中间的桥梁!但是不建议!
|
数数(计数) |
二进制 |
八进制 |
|
0 |
000 |
0 |
|
1 |
001 |
1 |
|
2 |
010 |
2 |
|
3 |
011 |
3 |
|
4 |
100 |
4 |
|
5 |
101 |
5 |
|
6 |
110 |
6 |
|
7 |
111 |
7 |
|
8 |
1000 |
10 |
|
9 |
1001 |
11 |
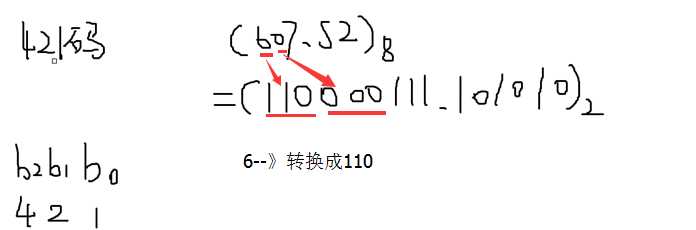
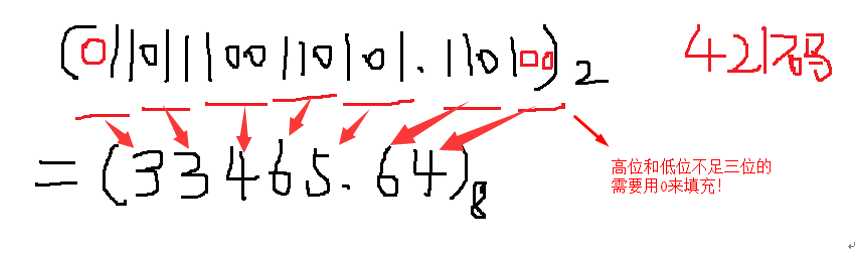
|
数数(计数) |
二进制 |
十六进制 |
|
0 |
0000 |
0 |
|
1 |
0001 |
1 |
|
2 |
0010 |
2 |
|
3 |
0011 |
3 |
|
4 |
0100 |
4 |
|
5 |
0101 |
5 |
|
6 |
0110 |
6 |
|
7 |
0111 |
7 |
|
8 |
1000 |
8 |
|
9 |
1001 |
9 |
|
10 |
1010 |
A |
|
11 |
1011 |
B |
|
12 |
1100 |
C |
|
13 |
1101 |
D |
|
14 |
1110 |
E |
|
15 |
1111 |
F |
|
16 |
10000 |
10 |
|
17 |
10001 |
11 |
所以:

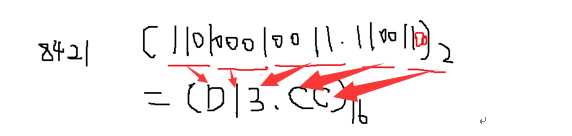
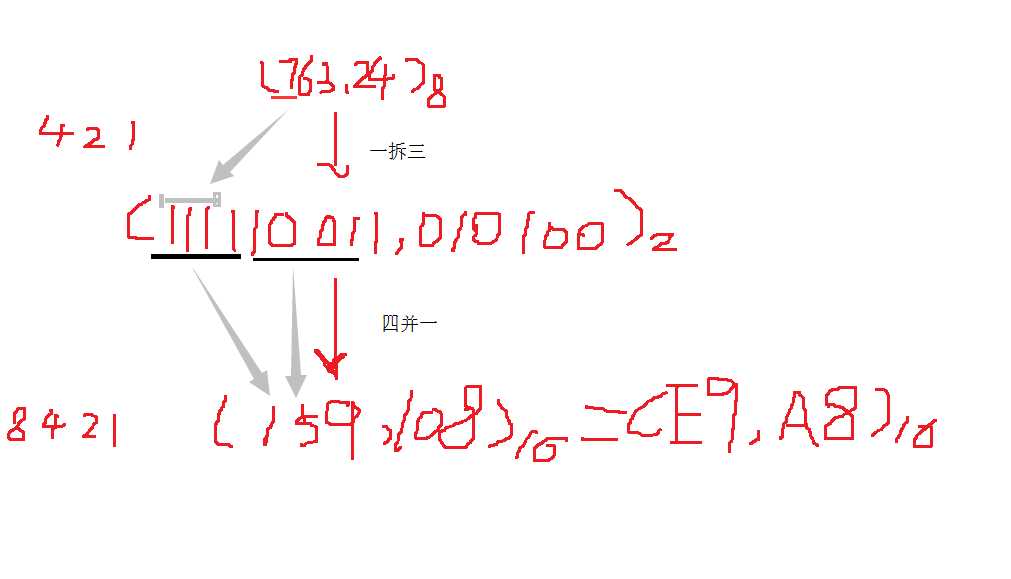
(763.24) 8 = (159.108)16=(E9.A8)16
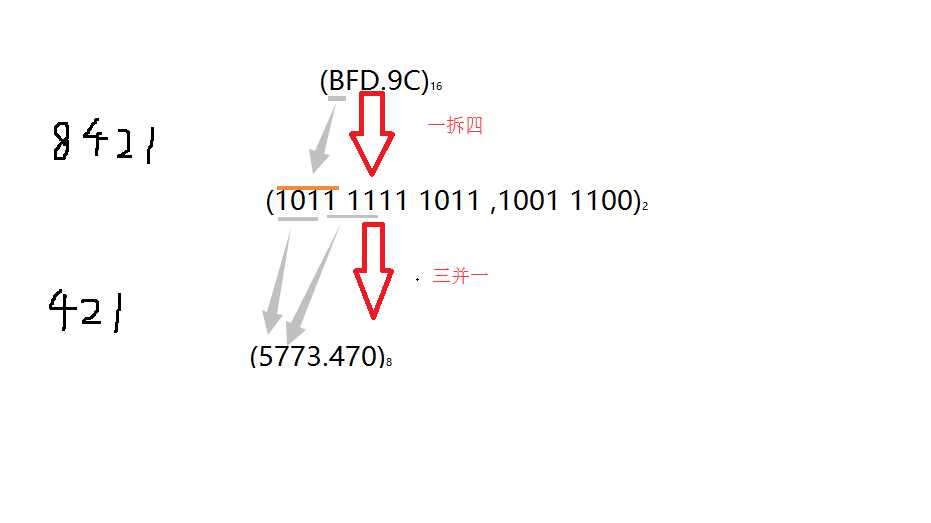
(BFD.9C)16 = (5773.470)8
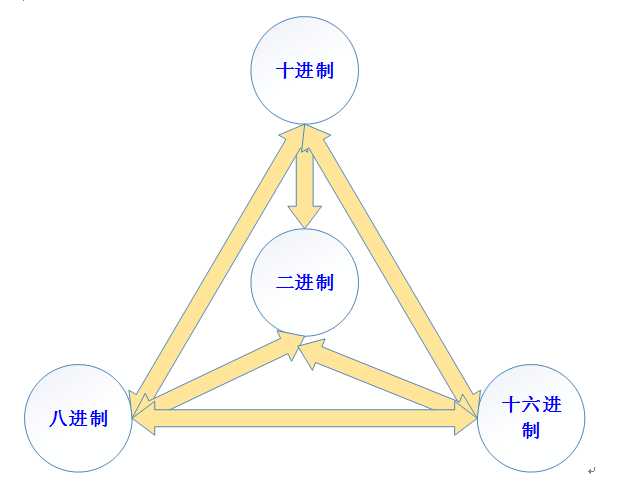
到了这里进制间的互相转换完毕
标签:十进制 0.11 16进制 有一个 结束 小数 精确 strong padding
原文地址:http://www.cnblogs.com/mrszhou/p/7425044.html