Zoj 3598 Spherical Triangle 【计算几何】【曲面三角形】

标签：计算几何   球面   

题目链接：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3598

题目大意：给出一个球体上的三点，三点的坐标以经纬度的形式给出，求曲面三角形的内角和。

即：给出ABC三个点的经纬度，求出 角A+ 角B+角C的值。

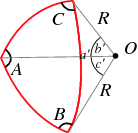
利用公式即可求得 cosa=cosb*cosc+sinb*sinc*cosA
其中小写a,b,c表示球面三角形边长所对应的圆心角 大写A表示三角形内角。

下面的难度就是求出abc角的大小即可。

网上看了一个写法看了好久看不太懂：T.T

<span style="font-size:14px;">//计算圆心角lat表示纬度,-90<=w<=90,lng表示经度
//返回两点所在大圆劣弧对应圆心角,0<=angle<=pi

double angle(double lng1, double lat1, double lng2, double lat2)
{
    double dlng = fabs(lng1 - lng2) * Pi / 180;
    while (dlng + eps > Pi + Pi)
        dlng -= Pi + Pi;
    if (dlng > Pi)
        dlng = Pi + Pi - dlng;
    lat1 *= Pi / 180, lat2 *= Pi / 180;
    return acos(cos(lat1) * cos(lat2) * cos(dlng) + sin(lat1) * sin(lat2));
}</span>

我们先把经纬度换为xyz坐标。（默认了R是1）

比如已知一点A的坐标为(x1,y1,z1)，B的坐标是(x2,y2,z2)
下面就是求角度AOB，向量OA为(x1,y1,z1)，向量OB为(x2,y2,z2)。

OA*OB=|OA|*|OB|*cos(角AOB)=x1*x2+y1*y2+z1*z2

则就可以求出角AOB了。

具体算法看代码：

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
const double PI = 2.0 * asin(1.0);
using namespace std;
struct po
{
    double x,y,z;
};

void m_change(double ll, double la, po& p)
{
    p.x = cos(la * PI / 180) * cos(ll * PI / 180);
    p.y = cos(la * PI / 180) * sin(ll * PI / 180);
    p.z = sin(la * PI / 180);
}

double xlj(po p, po q)
{
    return (p.x * q.x) + (p.y * q.y) + (p.z * q.z);
}

int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        po A,B,C;
        cin>>A.x>>A.y>>B.x>>B.y>>C.x>>C.y;
        m_change(A.x,A.y,A);
        m_change(B.x,B.y,B);
        m_change(C.x,C.y,C);

        double a = acos(xlj(C,B));
        double b = acos(xlj(A,C));
        double c = acos(xlj(A,B));
//        printf("a:%lf b:%lf c:%lf\n",a,b,c);

        double da,db,dc;
        da = acos((cos(a) - cos(b) * cos(c)) / (sin(b) * sin(c)));
        db = acos((cos(b) - cos(c) * cos(a)) / (sin(c) * sin(a)));
        dc = acos((cos(c) - cos(a) * cos(b)) / (sin(a) * sin(b)));
//        printf("da:%lf db:%lf dc:%lf\n",da,db,dc);
        double ans = da + db + dc;
        printf("%.2lf\n",ans * (180 / PI));
    }
}

Zoj 3598 Spherical Triangle 【计算几何】【曲面三角形】

标签：计算几何   球面   

原文地址：http://blog.csdn.net/u010468553/article/details/39081077