标签:style blog class code java tar
KMP 总结
1.strstr函数
|函数名: strstr |功 能: 在串中查找指定字符串的第一次出现 |用 法: char *strstr(char *str1, char *str2); |据说strstr和KMP的算法效率差不多
|注意:返回的是该字符串第一次出现时的指针,所以如果要计算下标,可以用原字符串首地址-返回的地址。
因为这样,还可以直接输出余下的字符串

1 int main() 2 { 3 char T[] = {"I love you ,do you know?"}; 4 char P[] = {"do"}; 5 printf("%s\n",strstr(T,P)); 6 return 0; 7 8 }
2.BF(朴素字符串匹配)

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 5 using namespace std; 6 7 //简单模式匹配算法 8 //Brute-Force (BF) 9 10 int search(char const* src,int slen,char const* patn,int plen) 11 { 12 int i = 0, j = 0; 13 while(i < slen && j < plen) 14 { 15 if(src[i] == patn[j]) 16 { 17 ++i; 18 ++j; 19 } 20 else 21 { 22 i = i - j + 1; 23 j = 0; 24 } 25 } 26 if(j >= plen) 27 return i - plen; 28 else 29 return -1; 30 } 31 32 33 int Index_BF(char* S,char* T,int pos) 34 { 35 int i = pos, j = 0; 36 while(S[i+j] && T[j]) 37 { 38 if(S[i+j] == T[j]) 39 j++; 40 else 41 i++,j=0; 42 } 43 if(!T[j]) 44 return i; 45 else 46 return -1; 47 } 48 49 50 int main() 51 { 52 char S[] = {"I love you ,do you know?"}; 53 char T[] = {"know"}; 54 int slen = strlen(S); 55 int tlen = strlen(T); 56 57 printf("%d\n",search(S,slen,T,tlen)); 58 printf("%d\n",Index_BF(S,T,0)); 59 60 return 0; 61 62 }
3.KMP算法
/* 我发现我原来对KMP确实没有理解到位。。 只能做一些KMP的模板题目真是很悲剧。。 KMP的意义不在于敲出模板, 而在鱼next数组的深刻理解,我只能说我现在有一点点理解了, 至于深刻不深刻我就不知道了 KMP优与BF算法的原因就在于充分利用了每一次匹配的信息, 通过预处理next数组,我们在时间上进行了很大的优化。 关于next数组的预处理, 虽然代码只有几行,但是值得研究的地方很多
void Get_nextval() { int k = -1, j = 0; CLR(next,0); next[0] = -1; while(j < Plen) { if(k == -1 || P[j] == P[k]) { k++; j++; // if(P[j] != P[k]) next[j] = k; // else next[j] = next[k]; // 这个地方到底要不要优化,其实是一个问题,优化之后不会有非常明显的省时间,不优化的话,可以体现很多next数组的性质和本质 next[j] = k; } else k = next[k]; } }
下面讨论next数组的性质,,原来一直没有理解透彻。
如果P为模式串,next是我们的预处理数组,显然next数组中存放的值是对应的P模式串中的一个位置
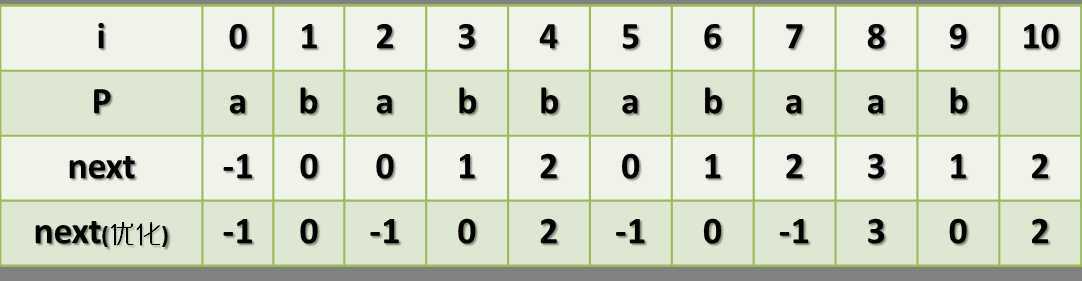
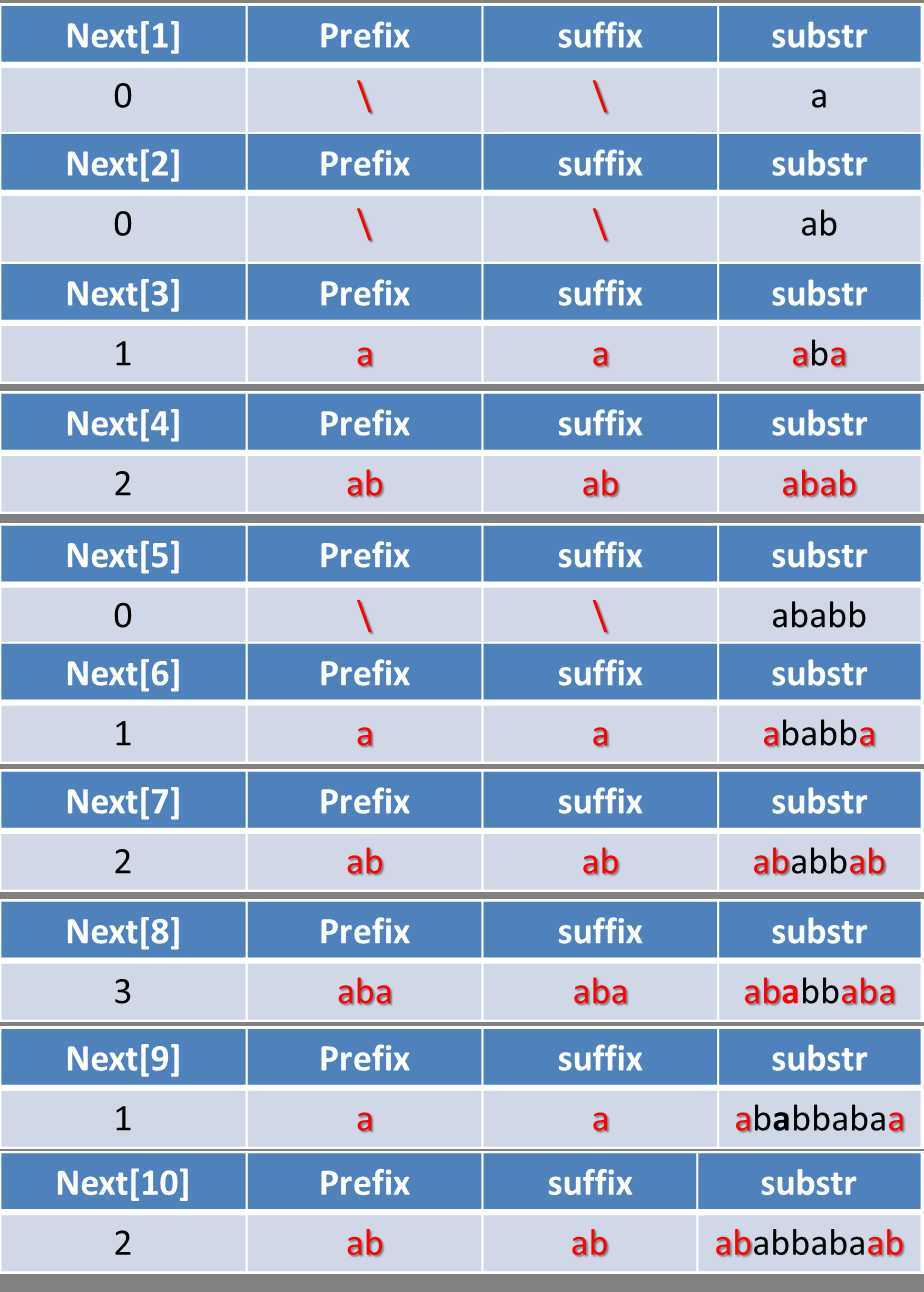
优化next和没有优化next,显然得到的值是不一样的。。事实上突然发现一半情况没有必要去优化。
优化之后很多性质肯能就无法使用了。
一般情况的模板题还是可以直接套用就是了。 */
KMP的精华在于它的next数组,, 先前也是只能写出代码但是对next数组的理解很不清晰。 对于字符串T 有 len(T) = L 若 x = next[i] 即 T[0...x-1] = T[L-x....L-1] 举两个实例: ① 对于 T = abaaba 有 L = 6 若取 x = next[3] = 3 则有 T[0...2] = T[3...5] 即 aba = aba 显然这是正确的 ② 对于 T = ababab 有 L = 6 若取 x = next[6] = 4 则有 T[0...3] = T[2...5] 即 abab = abab 显然这也是正确的 对于例②,为什么要举这个例子, 就是为了说明next[i]中的值必须是 使得子串T[0......M]中最大的前缀(并且这个前缀==后缀)
4.最小覆盖子串
参考资料: http://blog.csdn.net/fjsd155/article/details/6866991 最小覆盖子串的定义: 对于某个字符串S,存在子串P满足P自身通过多次重复连接得到串T,并且S为T的子串,且子串P长度最段,这样的的子串称为串S的最小覆盖子串。 例子: S = abcab P = abc T = abcabc 显然P为S的最小覆盖子串,T也满足定义 S = ababab P = ab T = ababab
证明引用
next[n]表明s[0,1,2,...,next[n]-1] == s[n-next[n],...,n-1],设这两段分别为s1和s2。 若s1和s2的长度之和小于s的长度,则说明s1和s2分别为不重叠的前缀和后缀,则最小覆盖子串必为s截去s2之后得到的前缀。 若s1和s2的长度之和大于等于s的长度,则最小覆盖子串也必为s截去s2之后得到的前缀。 以上两种情况都可以推出这个结论:最小覆盖子串是s的前缀,它的长度为n-next[n]。
最后可用的模板献上(Get_nextc处用了优化,其实真的不是很有必要)

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 5 using namespace std; 6 int Tlen,Plen; 7 8 void Get_nextval(char* P,int next[]) 9 { 10 int j = 0, k = -1; 11 next[0] = -1; 12 while(j < Plen) 13 { 14 if(k == -1 || P[j] == P[k]) 15 { 16 ++k; 17 ++j; 18 if(P[k] != P[j]) next[j] = k; 19 else next[j] = next[k]; 20 } 21 else 22 k = next[k]; 23 } 24 } 25 26 27 int KMP(char* T,char* P) 28 { 29 int next[100]; 30 int i = 0, j = 0; 31 32 Get_nextval(P,next); 33 34 while(i < Tlen && j < Plen) 35 { 36 if(j == -1 || T[i] == P[j]) 37 { 38 ++i; 39 ++j; 40 } 41 else 42 j = next[j]; 43 } 44 if(j == Plen) 45 return i - Plen; 46 else 47 return -1; 48 } 49 50 int main() 51 { 52 char T[] = {"I love you ,do you know?"}; 53 char P[] = {"do"}; 54 Tlen = strlen(T); 55 Plen = strlen(P); 56 57 int res = KMP(T,P); 58 printf("%d\n",res); 59 60 return 0; 61 62 }
1.HDU 1686 oulipo
//裸KMP。。可以直接用来当模板用,其实我就是直接套用的模板 //这里在KMP中扫整个Text串。res保存结果
//裸模板如下:

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 5 using namespace std; 6 #define CLR(a,b) memset(a,b,sizeof(a)) 7 8 int Tlen,Plen,N; 9 int next[10005]; 10 char text[1000005]; 11 char patn[10005]; 12 void Get_nextval(char* P,int next[]) 13 { 14 int j = 0, k = -1; 15 next[0] = -1; 16 while(j < Plen) 17 { 18 if(k == -1 || P[j] == P[k]) 19 { 20 ++k; 21 ++j; 22 if(P[k] != P[j]) next[j] = k; 23 else next[j] = next[k]; 24 } 25 else 26 k = next[k]; 27 } 28 } 29 30 int KMP(char* T,char* P) 31 { 32 int ans = 0; 33 CLR(next,0); 34 int i = 0, j = 0; 35 36 Get_nextval(P,next); 37 38 while(i < Tlen && j < Plen) 39 { 40 if(j == -1 || T[i] == P[j]) 41 { 42 ++i; 43 ++j; 44 } 45 else 46 j = next[j]; 47 48 if(j == Plen) 49 { 50 ++ans; 51 j = next[j]; 52 } 53 } 54 return ans; 55 } 56 57 58 int main() 59 { 60 scanf("%d",&N); 61 62 while(N--) 63 { 64 scanf("%s",patn); 65 scanf("%s",text); 66 Tlen = strlen(text); 67 Plen = strlen(patn); 68 int res = KMP(text,patn); 69 printf("%d\n",res); 70 } 71 72 return 0; 73 }
2.HDU 2087 剪花布条
//裸KMP, //这题要注意和1686进行比较
if(j == Plen) { cnt++; // j = next[j]; 这样的话是错误的。 j = 0; }

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 5 using namespace std; 6 #define CLR(a,b) memset(a,b,sizeof(a)) 7 int Tlen, Plen, cnt; 8 int next[1005]; 9 char T[1005],P[1005]; 10 11 void Get_nextval(char* P,int next[]) 12 { 13 int j = 0, k = -1; 14 CLR(next,0); 15 next[0] = -1; 16 while(j < Plen) 17 { 18 if(k == -1 || P[j] == P[k]) 19 { 20 ++k; 21 ++j; 22 if(P[k] != P[j]) next[j] == k; 23 else next[j] = next[k]; 24 } 25 else 26 k = next[k]; 27 } 28 } 29 30 31 void KMP(char* T,char* P) 32 { 33 int i = 0, j = 0; 34 Get_nextval(P,next); 35 36 while(i < Tlen && j < Plen) 37 { 38 if(j == -1 || T[i] == P[j]) 39 { 40 ++i; 41 ++j; 42 } 43 else 44 j = next[j]; 45 46 if(j == Plen) 47 { 48 cnt++; 49 // j = next[j]; 这样的话是错误的。 50 j = 0; 51 } 52 } 53 } 54 55 int main() 56 { 57 while(scanf("%s",T)!=EOF && *T!=‘#‘) 58 { 59 scanf("%s",P); 60 Tlen = strlen(T); 61 Plen = strlen(P); 62 cnt = 0; 63 KMP(T,P); 64 printf("%d\n",cnt); 65 } 66 67 return 0; 68 }
3.HDU 1711 Number sequence
//好吧,这题裸得更厉害。。。。。 //直接KMP的

1 #include<cstdio> 2 #include<cstring> 3 4 5 using namespace std; 6 #define CLR(a,b) memset(a,b,sizeof(a)) 7 8 int Tlen, Plen; 9 int text[1000005]; 10 int patn[10005]; 11 int next[10005]; 12 int N,m,n,res; 13 14 void Get_nextval(int* P,int next[]) 15 { 16 CLR(next,0); 17 int j = 0, k = -1; 18 next[0] = -1; 19 while(j < Plen) 20 { 21 if(k == -1 || P[j] == P[k]) 22 { 23 ++k; 24 ++j; 25 if(P[k] != P[j]) next[j] = k; 26 else next[j] = next[k]; 27 } 28 else 29 k = next[k]; 30 } 31 } 32 33 int KMP(int* T, int* P) 34 { 35 int i = 0, j = 0; 36 Get_nextval(P,next); 37 38 while(i < Tlen && j < Plen) 39 { 40 if(j == -1 || T[i] == P[j]) 41 { 42 ++i; 43 ++j; 44 } 45 else 46 j = next[j]; 47 } 48 if(j == Plen) 49 return i - Plen; 50 else 51 return -1; 52 } 53 54 int main() 55 { 56 scanf("%d",&N); 57 while(N--) 58 { 59 scanf("%d %d",&m,&n); 60 for(int i=0;i<m;i++) 61 scanf("%d",&text[i]); 62 for(int j=0;j<n;j++) 63 scanf("%d",&patn[j]); 64 Tlen = m; 65 Plen = n; 66 res = KMP(text,patn); 67 if(res != -1) 68 printf("%d\n",res+1); 69 else 70 printf("-1\n"); 71 } 72 return 0; 73 }
4.HDU 2203 亲和数
//同水,,,但是一开始还是错了。。 //一开始是一位一位移动,再进行KMP,果断超时 //后来直接复制一份到数组后面,直接一次KMP搞定。

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 5 using namespace std; 6 #define CLR(a,b) memset(a,b,sizeof(a)) 7 int Tlen, Plen; 8 char Tmp[100005],P[100005*2],T[100005*2]; 9 int next[100005*2]; 10 void Get_nextval(char* P,int next[]) 11 { 12 CLR(next,0); 13 int j = 0, k = -1; 14 next[0] = -1; 15 while(j < Plen) 16 { 17 if(k == -1 || P[j] == P[k]) 18 { 19 ++k; 20 ++j; 21 if(P[j] != P[k]) next[j] = k; 22 else next[j] = next[k]; 23 } 24 else 25 k = next[k]; 26 } 27 } 28 29 int KMP(char* T,char* P) 30 { 31 int i = 0, j = 0; 32 Get_nextval(P,next); 33 34 while(i < Tlen && j < Plen) 35 { 36 if(j == -1 || T[i] == P[j]) 37 { 38 ++i; 39 ++j; 40 } 41 else 42 j = next[j]; 43 } 44 if(j == Plen) 45 return 1; 46 else 47 return 0; 48 } 49 50 int main() 51 { 52 while(scanf("%s %s",Tmp,P)!=EOF) 53 { 54 Tlen = strlen(Tmp); 55 strcpy(T,Tmp); 56 strcpy(T+Tlen,Tmp); 57 Tlen = strlen(T); 58 Plen = strlen(P); 59 if(KMP(T,P)) 60 puts("yes"); 61 else 62 puts("no"); 63 } 64 65 return 0; 66 }
5.POJ 2406 Power Strings
刚开始理解KMP的时候对这种题目是没有感觉的。
只知道一个结论就是
最小覆盖子串 L = len - next[len];
后来才知道这个是正确的。
知道这个之后,这题的思路就是先预处理next数组,求出最小覆盖子串。
如果len % L = 0 , 说明了最小循环节存在(也就是最小覆盖子串)
如果len % L ≠ 0, 那就输出1,表示没有循环节。。

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 5 using namespace std; 6 #define CLR(a,b) memset(a,b,sizeof(a)) 7 8 char P[1000010]; 9 int next[1000010]; 10 int Plen,L; 11 12 void Get_nextval() 13 { 14 int k = -1, j = 0; 15 CLR(next,0); 16 next[0] = -1; 17 Plen = L = strlen(P); 18 while(j < Plen) 19 { 20 if(k == -1 || P[j] == P[k]) 21 { 22 ++j; 23 ++k; 24 next[j] = k; 25 } 26 else 27 k = next[k]; 28 } 29 L = L - next[L]; 30 if(Plen % L == 0) 31 { 32 printf("%d\n",Plen/L); 33 } 34 else 35 printf("1\n"); 36 } 37 38 int main() 39 { 40 while(scanf("%s",P) && *P!=‘.‘) 41 { 42 Get_nextval(); 43 } 44 return 0; 45 }
6.POJ 2752 Seek the Name Seek the Fram
再次考察的是KMP next数组的性质。 在了解了next数组的实质之后。会明白next[x]中存放的值就是对应的子串中前缀和后缀相等的数量。 例如题目给出的串 ababcababababcabab next数组的值分别为 -1,0,0,1,2,0,1,2,3,4,3,4,3,4,5,6,7,8,9 通过从最后一个next[n]开始进行回溯,直到最后next[i] = 0 结束 参考:http://blog.csdn.net/a402630999/article/details/720825

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 5 using namespace std; 6 #define CLR(a,b) memset(a,b,sizeof(a)) 7 8 char P[400004]; 9 int next[400004]; 10 int Hash[400004]; 11 int Plen,L,cnt; 12 13 void Get_nextval() 14 { 15 int k = -1, j = 0; 16 Plen = strlen(P); 17 CLR(next,0); 18 next[0] = -1; 19 20 while( j < Plen ) 21 { 22 if(k == -1 || P[j] == P[k]) 23 { 24 ++k; 25 ++j; 26 next[j] = k; 27 } 28 else 29 k = next[k]; 30 } 31 } 32 void solve() 33 { 34 Get_nextval(); 35 CLR(Hash,0); 36 L = Plen; 37 cnt = 0; 38 while(next[L]) 39 { 40 Hash[cnt++] = next[L];; 41 L = next[L]; 42 } 43 for(int i=cnt-1;i>=0;i--) 44 { 45 printf("%d ",Hash[i]); 46 } 47 printf("%d\n",Plen); 48 } 49 50 int main() 51 { 52 while(scanf("%s",P)!=EOF) 53 { 54 solve(); 55 } 56 57 return 0; 58 }
7.HDU 3746 Cyclic Nacklace
考察next数组的性质
在理解了最小覆盖子串的情况下这道题做出来还是比较顺利的
设字符串总长L
首先找到最小覆盖子串Lmin = L - next[L],
然后用总长度 L%Lmin --> t
且循环次数 K = L/Lmin, (题目要求循环结至少出现两次)
如果 t = 0 && K>=2 说明该串不需要再增加珍珠了,
如果 t ≠ 0 说明有余数。那么就需要在串的末尾加上若干的珍珠。
int L = Plen - next[Plen]; if(Plen%L || Plen/L < 2) printf("%d\n",L - Plen%L); else printf("0\n");

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 5 using namespace std; 6 #define CLR(a,b) memset(a,b,sizeof(a)) 7 8 int Plen,Tlen,N; 9 char P[100010]; 10 int next[100010]; 11 void Get_nextval() 12 { 13 CLR(next,0); 14 int k = -1, j = 0; 15 next[0] = -1; 16 Plen = strlen(P); 17 while(j < Plen) 18 { 19 if(k == -1 || P[j] == P[k]) 20 { 21 ++k; 22 ++j; 23 next[j] = k; 24 } 25 else 26 k = next[k]; 27 } 28 int L = Plen - next[Plen]; 29 if(Plen%L || Plen/L < 2) 30 printf("%d\n",L - Plen%L); 31 else 32 printf("0\n"); 33 } 34 35 36 int main() 37 { 38 scanf("%d",&N); 39 while(N--) 40 { 41 scanf("%s",P); 42 Get_nextval(); 43 } 44 45 return 0; 46 }
8.HDU 1358 Period
刚开始也想到了next数组的性质。 但是还是傻逼得用来N次next数组构造去做,果断超时了。 这里对字符串进行一次next数组的处理, 然后都next数组进行n-1次扫描。(从2开始,而且是前缀) 满足是周期就输出当前字符串长度 和 周期出现次数。

1 //考虑下这题,应该是先对串S进行每一个前缀的检查,构建next数组,然后找循环节,根据题意输出 2 //前缀的坚持直接通过next数组的性质。。。最小覆盖子串 3 #include<cstdio> 4 #include<cstring> 5 #include<algorithm> 6 7 using namespace std; 8 #define CLR(a,b) memset(a,b,sizeof(a)) 9 10 char P[1000010]; 11 int Plen,N,K,cnt; 12 int next[1000010]; 13 14 void Get_nextval() 15 { 16 CLR(next,0); 17 int k = -1, j = 0; 18 next[0] = -1; 19 Plen = strlen(P); 20 while(j < Plen) 21 { 22 if(k == -1 || P[j] == P[k]) 23 { 24 ++j; 25 ++k; 26 next[j] = k; 27 } 28 else 29 k = next[k]; 30 } 31 } 32 33 void solve() 34 { 35 Get_nextval(); 36 for(int i=2;i<=N;i++) 37 { 38 int L = i - next[i]; 39 if(i%L == 0) 40 { 41 K = i/L; 42 if(K >= 2) 43 printf("%d %d\n",i,K); 44 } 45 } 46 } 47 48 int main() 49 { 50 cnt = 0; 51 while(scanf("%d",&N)!=EOF && N) 52 { 53 scanf("%s",P); 54 printf("Test case #%d\n",++cnt); 55 solve(); 56 printf("\n"); 57 } 58 return 0; 59 }
9.POJ Blue Jeans
这道题WA了多次,一开始觉得没有必要使用flag,结果一直WA,后来没有 处理好循环,还在WA。。最后调试之后终于AC。
思路:
首先读入所有的DNA序列,枚举第一个DNA序列的所有子串。
以此对剩下的所有NDA序列进行KMP,如果成功,记录长度,判断是否更新res数组和maxlen,最后输出

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 5 using namespace std; 6 #define CLR(a,b) memset(a,b,sizeof(a)) 7 8 int M,N,Tlen,Plen,maxlen,flag; 9 int next[100]; 10 char str[10][100]; 11 char tmp[100],res[100]; 12 13 void Get_nextval(char* P) 14 { 15 CLR(next,0); 16 next[0] = -1; 17 int k = -1, j = 0; 18 Plen = strlen(P); 19 while(j < Plen) 20 { 21 if(k == -1 || P[k] == P[j]) 22 { 23 ++k; 24 ++j; 25 next[j] = k; 26 } 27 else 28 k = next[k]; 29 } 30 } 31 32 bool KMP(char* T,char* P) 33 { 34 Get_nextval(P); 35 int i = 0, j = 0; 36 Tlen = strlen(T); 37 while(i < Tlen && j < Plen) 38 { 39 if(j == -1 || T[i] == P[j]) 40 { 41 ++i; 42 ++j; 43 } 44 else 45 j = next[j]; 46 } 47 if(j == Plen) 48 return true; 49 else 50 return false; 51 } 52 53 void solve() 54 { 55 scanf("%d",&M); 56 for(int i=0;i<M;i++) 57 scanf("%s",str[i]); 58 maxlen = -1; 59 for(int i=0;i<=60-3;i++) 60 { 61 for(int j=i+3;j<=60;j++) 62 { 63 CLR(tmp,‘\0‘); 64 strncpy(tmp,str[0]+i,j-i); 65 flag = 1; 66 for(int k=1;k<M;k++) 67 { 68 if(!KMP(str[k],tmp)) 69 { 70 flag = 0; 71 break; 72 } 73 } 74 if(flag) 75 { 76 int len = strlen(tmp); 77 if(maxlen < len) 78 { 79 strcpy(res,tmp); 80 maxlen = len; 81 } 82 else if(maxlen == len && strcmp(res,tmp) > 0) 83 { 84 strcpy(res,tmp); 85 } 86 } 87 } 88 } 89 if(maxlen >= 3) 90 printf("%s\n",res); 91 else 92 printf("no significant commonalities\n"); 93 } 94 95 int main() 96 { 97 while(scanf("%d",&N)!=EOF) 98 { 99 while(N--) 100 { 101 solve(); 102 } 103 } 104 }
10.HDU 4300 Clairewds‘s Massage(扩展KMP)
这题先写思路吧,接触到了扩展KMP还不会写。。 题目大意: 给定义个密码表(可将密文翻译为明文) 再给定一个text 这个text一定是恰由密文和明文组成的,但是可能是截断的 也就是说,text 前面部分是密文,后面部分是明文。(由于可能截断,所以明文不一定完整,但是密文是完整的) 求出长度最小的完整的text字符串。 开始想用KMP,从len/2开始。这题可以暴力过,但是我的代码可能有问题。 有一种思路非常好,Blog:http://blog.csdn.net/libin56842/article/details/8504523
标签:style blog class code java tar
原文地址:http://www.cnblogs.com/BigBallon/p/3671462.html