正规方程法

标签：效率   线性回归   mil   两种   注意   es2017   公式   函数   计算机   

前言

           以下内容是个人学习之后的感悟，如果有错误之处，还请多多包涵~

正规方程法

一、函数参数向量化

         在计算机中，我们需要用同样的算法计算大量数据样本时，一般有两种方式：循环、参数向量化。

         循环~，可想而知，计算量不是一般的大，不建议。

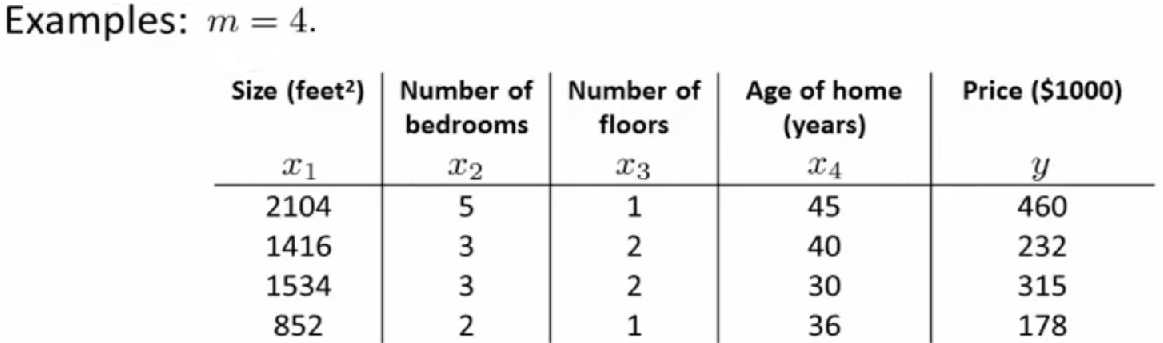
         参数向量化的效率就高多了，把全部样本转换为向量，一次执行就搞定了。具体向量化方法，如下图所示，以线性回归

方程h_θ(x)=θ₀+θ₁x₁为例，最终转换为θ的等价公式，为正规方程法做好准备。

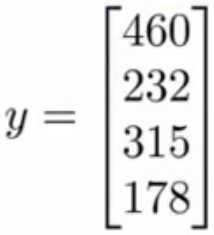
二、正规方程法

        直接根据上图中的θ等价公式，采用所给样本，进行矩阵运算即可。

        注意：由于矩阵的特殊性，以下三点需要谨慎对待。

• 矩阵（X^TX）不可逆

                原因1：所求参数大于样本数。

                措施  ：增加样本数。

                原因2：特征值太多。

                措施  ：删除一些冗余的特征值。

• 样本量n太大

                 矩阵求逆的计算复杂度为O(n³)，当样本量太大时，计算量过大，此时，不建议采用正规方程法。

• 函数太复杂

                此时无法使用正规方程法。

以上是全部内容，如果有什么地方不对，请在下面留言，谢谢~

正规方程法

标签：效率   线性回归   mil   两种   注意   es2017   公式   函数   计算机   

原文地址：http://www.cnblogs.com/steed/p/7434864.html