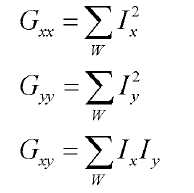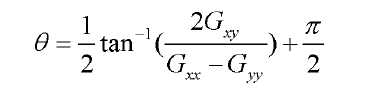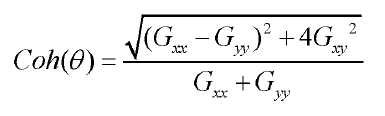//变量
Mat img = cv::imread( "e:/template/finger.bmp",0);
Mat matX;Mat matY;
Mat Gxx;Mat Gyy;Mat Gxy;//和论文标识对应
Mat matTheta;//方向场
Mat matCoh;//方向场一致性
//实验图片
/*Mat matTst = Mat(Size(11,11),CV_8UC1,Scalar(0));
line(matTst,Point(5,0),Point(5,11),Scalar(255));
line(matTst,Point(0,5),Point(11,5),Scalar(255));*/
Mat matTst = img.clone();
//x方向求导
Sobel(matTst,matX,CV_16SC1,1,0);
//y方向求导
Sobel(matTst,matY,CV_16SC1,0,1);
//转换为float计算，否则后面算爆掉
matX.convertTo(matX,CV_32FC1);
matY.convertTo(matY,CV_32FC1);
//计算3个G
Gxx = matX.mul(matX);
Gyy = matY.mul(matY);
Gxy = matX.mul(matY);
Mat kernel8 = Mat(Size(8,8),CV_32FC1,Scalar(1));
filter2D(Gxx,Gxx,Gxx.depth(),kernel8);
filter2D(Gyy,Gyy,Gyy.depth(),kernel8);
filter2D(Gxy,Gxy,Gxy.depth(),kernel8);
//计算方向场
Mat matTmp = 2 * Gxy;
matTmp = matTmp / (Gxx - Gxy);
matTheta = Mat(matTst.size(),CV_32FC1,Scalar(0));
for (int i = 0 ;i< matTmp.rows;i++)
for (int j = 0 ;j<matTmp.cols;j++)
matTheta.at<float>(i,j) = 0.5 * atan(matTmp.at<float>(i,j)) + 3.1415926/2;
//计算方向场一致性
matTmp = Gxx - Gyy;
matTmp = matTmp.mul(matTmp);
Mat matTmp2 = 4*Gxy.mul(Gxy);
matTmp += matTmp2;
cv::sqrt(matTmp,matCoh);
matCoh = matCoh / (Gxx+Gxy);
//显示结果
normalize(matTheta,matTheta,0,1,NORM_MINMAX);
normalize(matCoh,matCoh,0,1,NORM_MINMAX);//hessian方法
frangi2d_opts_t opts;
opts.sigma_start = DEFAULT_SIGMA_START;
opts.sigma_end = DEFAULT_SIGMA_END;
opts.sigma_step = DEFAULT_SIGMA_STEP;
opts.BetaOne = DEFAULT_BETA_ONE; //ignore blob-like structures?
opts.BetaTwo = DEFAULT_BETA_TWO; //appropriate background suppression for this specific image, but can change.
opts.BlackWhite = true;
Mat J;Mat Scale;Mat directions;
img.convertTo(img,CV_32FC1,1.0/255);
frangi2d(img,J,Scale,directions,opts);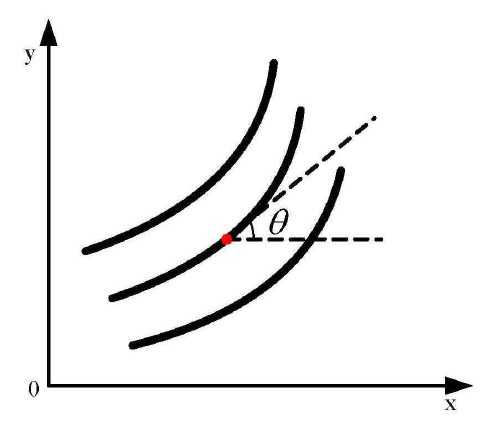
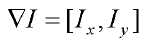，表示x方向的梯度和y方向的梯度
