【洛谷P1641】[SCOI2010]生成字符串

标签：输入数据   lan   long   color   base   pre   ati   ext   组成   

题目描述

lxhgww最近接到了一个生成字符串的任务，任务需要他把n个1和m个0组成字符串，但是任务还要求在组成的字符串中，在任意的前k个字符中，1的个数不能少于0的个数。现在lxhgww想要知道满足要求的字符串共有多少个，聪明的程序员们，你们能帮助他吗？

输入输出格式

输入格式：

输入数据是一行，包括2个数字n和m

输出格式：

输出数据是一行，包括1个数字，表示满足要求的字符串数目，这个数可能会很大，只需输出这个数除以20100403的余数

输入输出样例

2 2

2

说明

limitation

每点2秒

对于30%的数据，保证1<=m<=n<=1000

对于100%的数据，保证1<=m<=n<=1000000

来源：SCOI 2010

分析(转载)

原文地址

写的确实不错。

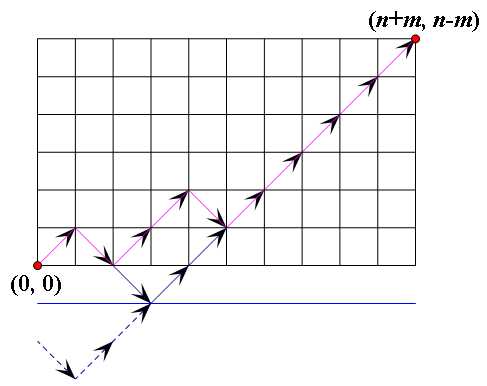
首先，我们设选1为(1,1),选0为(1,-1)

目标就是(n+m,n-m)

总方案数为C(n+m,n)，因为有n+m个位置，放n个1

然后要减去不合法的即线路通过y=-1的。将线路与y=-1交点的左边沿着y=-1做对称操作，则最后等价于从(0,-2)走到(n+m,n-m)的方案数

所以向上走n-m+2

则有x-y=n-m+2

　　x+y=n+m

　　x=n+1,y=m-1

所以不合法方案为C(n+m,n+1)

ans=C(n+m,n)-C(n+m,n+1)

求这些用模逆元，O(n)求解

另附上洛谷题解中的分析

原文地址

可以考虑把11的个数与00的个数的和看成xx坐标，11的个数与00的个数的差看成yy坐标，那么如下图：

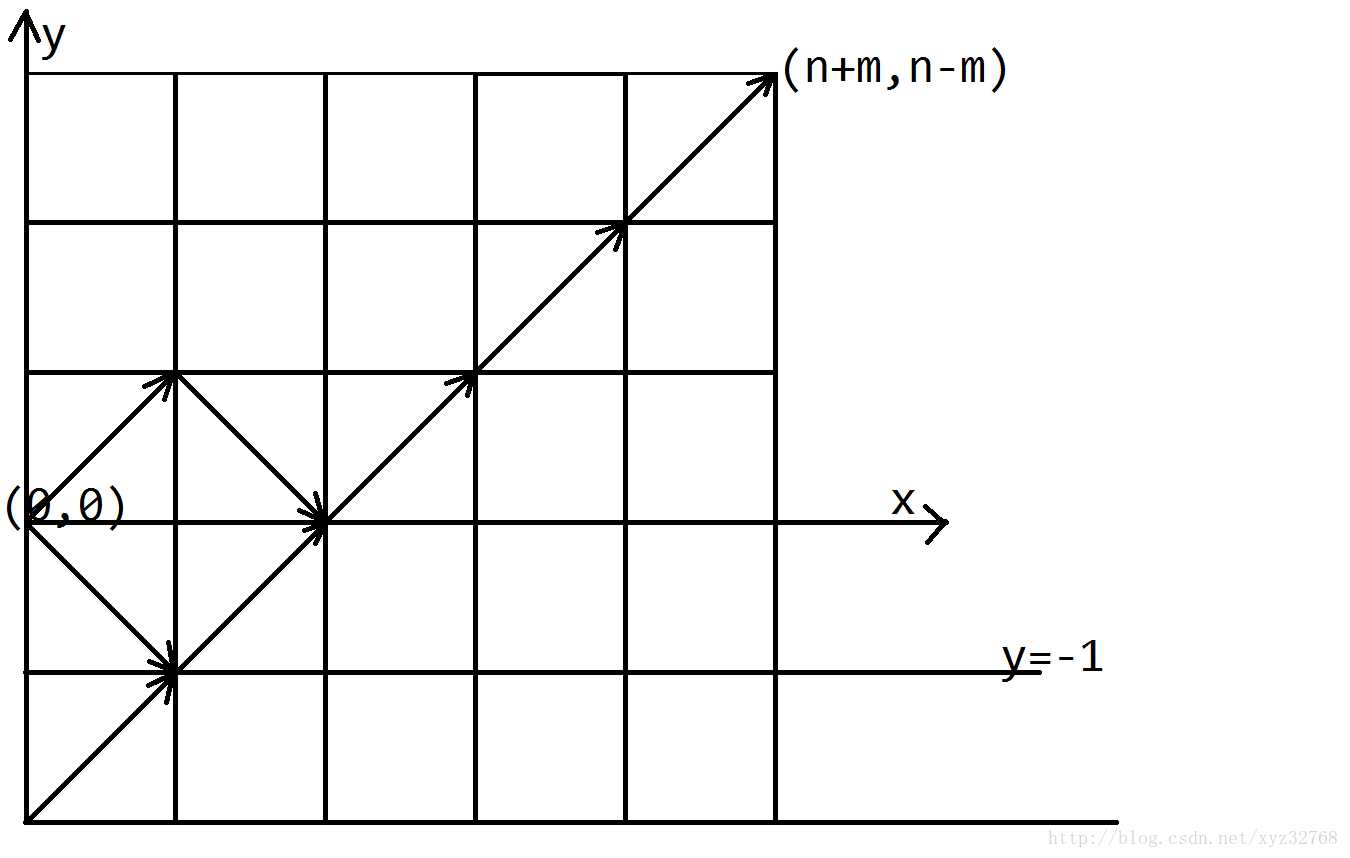
向右上走（xx坐标加11，yy坐标加11）就表示这个字符选择11。

向右下走（xx坐标加11，yy坐标减11）就表示这个字符选择00。

这样子，如果不考虑限制条件，就表示从(0,0)(0,0)走n+mn+m步到达(n+m,n-m)(n+m,n?m)，这相当于从n+mn+m步中选出mm步向右下走，也就是C(n+m,m)C(n+m,m)。

考虑限制条件，任意前缀中11的个数不少于00的个数，也就是这条路径不能经过直线y=-1y=?1。可以通过对称性发现，从(0,0)(0,0)走到直线y=-1y=?1上的一点，相当于从(0,-2)(0,?2)走到该点。也就是说，路径经过直线y=-1y=?1的方案数就是从(0,-2)(0,?2)走n+mn+m步到达(n+m,n-m)(n+m,n?m)，这个方案数可以用组合数表示为C(n+m,m-1)C(n+m,m?1)。

所以最后结果为C(n+m,m)-C(n+m,m-1)C(n+m,m)?C(n+m,m?1)。对于组合数，可以预处理阶乘后用乘法逆元计算。

代码

我是用费马小定理做的

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int p=20100403;
typedef long long ll;
int n,m;
int fac[2000005];
int power(int a,int b)
{
    int res=1,base=a;
    while(b)
    {
        if(b&1) res=(ll)res*(ll)base%(ll)p;
        base=(ll)base*(ll)base%(ll)p;
        b=b>>1;
    }
    return res;
}
int inv(int x)
{ return power(x,p-2);}
void fct()
{
    fac[0]=1;
    for(int i=1;i<=2000000;i++)
        fac[i]=(ll)fac[i-1]*(ll)i%(ll)p;
}
int main()
{
    scanf("%d%d",&n,&m);
    fct();
    int t1,t2,x1,x2,ans;
    t1=fac[n+m];
    t2=(ll)fac[n]*(ll)fac[m]%(ll)p;
    x1=(ll)t1*(ll)inv(t2)%(ll)p;
    t2=(ll)fac[m-1]*(ll)fac[n+1]%(ll)p;
    x2=(ll)t1*(ll)inv(t2)%(ll)p;
    ans=(x1%p-x2%p+p)%p;
    printf("%d\n",ans);
    return 0;
}
    

【洛谷P1641】[SCOI2010]生成字符串

标签：输入数据   lan   long   color   base   pre   ati   ext   组成   

原文地址：http://www.cnblogs.com/huihao/p/7449960.html