标签:com cos mina any point pre str uniq proc
Latent semantic analysis (LSA) is a technique in natural language processing, in particular distributional semantics, of analyzing relationships between a set of documents and the terms they contain by producing a set of concepts related to the documents and terms. LSA assumes that words that are close in meaning will occur in similar pieces of text (the distributional hypothesis). A matrix containing word counts per paragraph (rows represent unique words and columns represent each paragraph) is constructed from a large piece of text and a mathematical technique called singular value decomposition (SVD) is used to reduce the number of rows while preserving the similarity structure among columns. Words are then compared by taking the cosine of the angle between the two vectors (or the dot product between the normalizations of the two vectors) formed by any two rows. Values close to 1 represent very similar words while values close to 0 represent very dissimilar words.
Occurrence matrix:
LSA can use a term-document matrix which describes the occurrences of terms in documents; it is a sparse matrix whose rows correspond to terms and whose columns correspond to documents. A typical example of the weighting of the elements of the matrix is tf-idf (term frequency–inverse document frequency): the weight of an element of the matrix is proportional to the number of times the terms appear in each document, where rare terms are upweighted to reflect their relative importance.
Rank lowering:
After the construction of the occurrence matrix, LSA finds a low-rank approximation[4] to the term-document matrix. There could be various reasons for these approximations:
Derivation
Let $X$ be a matrix where element $ (i,j)$ describes the occurrence of term $ i $ in document $j$ (this can be, for example, the frequency). $X$ will look like this:

Now a row in this matrix will be a vector corresponding to a term, giving its relation to each document:

Likewise, a column in this matrix will be a vector corresponding to a document, giving its relation to each term:

Now, from the theory of linear algebra, there exists a decomposition of $X$ such that $U$ and $ V $ are orthogonal matrices and $\Sigma$ is a diagonal matrix. This is called a singular value decomposition (SVD):

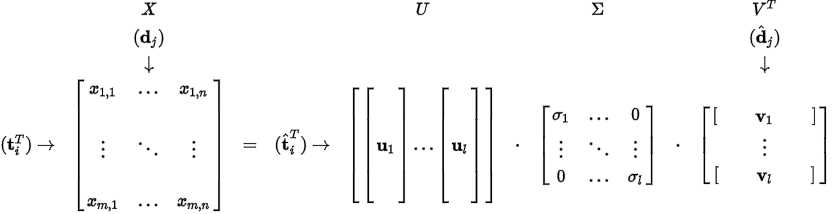
The values {\displaystyle \sigma _{1},\dots ,\sigma _{l}} \sigma _{1},\dots ,\sigma _{l} are called the singular values, and {\displaystyle u_{1},\dots ,u_{l}} u_{1},\dots ,u_{l} and {\displaystyle v_{1},\dots ,v_{l}} v_{1},\dots ,v_{l} the left and right singular vectors. Notice the only part of {\displaystyle U} U that contributes to {\displaystyle {\textbf {t}}_{i}} {\textbf {t}}_{i} is the {\displaystyle i{\textrm {‘th}}} i{\textrm {‘th}} row. Let this row vector be called {\displaystyle {\hat {\textrm {t}}}_{i}^{T}} {\displaystyle {\hat {\textrm {t}}}_{i}^{T}}. Likewise, the only part of {\displaystyle V^{T}} V^{T} that contributes to {\displaystyle {\textbf {d}}_{j}} {\textbf {d}}_{j} is the {\displaystyle j{\textrm {‘th}}} j{\textrm {‘th}} column, {\displaystyle {\hat {\textrm {d}}}_{j}} {\hat {\textrm {d}}}_{j}. These are not the eigenvectors, but depend on all the eigenvectors.
It turns out that when you select the {\displaystyle k} k largest singular values, and their corresponding singular vectors from {\displaystyle U} U and {\displaystyle V} V, you get the rank {\displaystyle k} k approximation to {\displaystyle X} X with the smallest error (Frobenius norm). This approximation has a minimal error. But more importantly we can now treat the term and document vectors as a "semantic space". The row "term" vector {\displaystyle {\hat {\textbf {t}}}_{i}^{T}} {\displaystyle {\hat {\textbf {t}}}_{i}^{T}} then has {\displaystyle k} k entries mapping it to a lower-dimensional space dimensions. These new dimensions do not relate to any comprehensible concepts. They are a lower-dimensional approximation of the higher-dimensional space. Likewise, the "document" vector {\displaystyle {\hat {\textbf {d}}}_{j}} {\hat {\textbf {d}}}_{j} is an approximation in this lower-dimensional space. We write this approximation as

https://en.wikipedia.org/wiki/Latent_semantic_analysis
标签:com cos mina any point pre str uniq proc
原文地址:http://www.cnblogs.com/ljygoodgoodstudydaydayup/p/7450225.html